二进制的（位）运算及其应用

introduction

正负数的二进制表示、存储与运算，Java位运算，Java运算符的优先级，及其相关应用。

Ⅰ Expression of Binary Digit 二进制数的表示方式

二进制（binary）在数学和数字电路中指以2为基数的记数系统，以2为基数代表系统是二进位制的。这一系统中，通常用两个不同的数字0和1来表示。数字电子电路中，逻辑门直接采用了二进制，因此现代的计算机和依赖计算机的设备里都用到二进制。每个数字称为一个比特（Bit，Binary digit 的缩写）。二进制表示从0开始，“逢二进一”（N进制则逢N进一）。例如对于十进制的0、1、2，二进制表示为0、1、10。

二进制 -> 十进制：

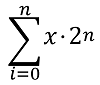
其中 n 表示从低位往高位的位数(从0开始)，x 表示对应位数上的值(1 或 0)，例如101101 = 1 * 2^0 + 0 * 2^1 + 1 * 2^2 + 1 * 2^3 + 0 * 2^4 + 1 * 2^5 = 1+0+4+8+0+32=45
十进制 -> 二进制：
1) 使用除法求余数的方式

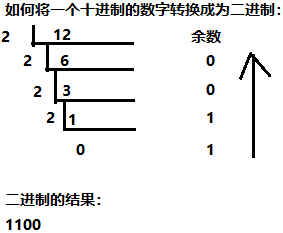
2) 使用反推的方式
将十进制数N转换为二进制，首先找到一个最接近且小于等于N的2的乘方的数m（即m=2^x，x为整数），其二进制对应x位上则为1，其次对十进制数N-m重复此步骤，直到N-m等于1或0。例如将十进制数168转换为二进制：
ㅤㅤa) 找到最接近且小于等于168的2的乘方的数为128（2^7），故二进制数的第7位为1（10000000）
ㅤㅤb) 对40（168-128），找到32（2^5），故第5位为1（10100000）
ㅤㅤc) 对8（40-32），找到8（2^3），故第3位为1（10101000）
ㅤㅤd) 对0（8-82），此时为0，二进制数第0位为0
最终结果为：168=128+32+8 -> 10101000。

Ⅱ Storage and Operation of Binary Digit 二进制数的存储与运算

1. Signed Binary Digit 有符号的二进制数

一个有符号的二进制数，其最高位为符号位，1表示负，0表示正，剩余位为数值域。故对于一个字节(8位)，无符号可以表示2^8个(其范围为：0~2^8-1)不同的数，但如果为有符号数，则需要将最高位来表示符号位，虽然同样可以表示2^8个数，但是表示范围变为了：-2^7 ~ 2^7-1。

2. True Form, One’s Complement and Two’s Complement 原码、反码及补码

正数：原码、反码、补码都是其本身
负数：原码是其本身；反码由原码符号位不变，其它位取反得到；补码=反码+1。
例如二进制数10010001：原码=10010001；反码=11101110；补码=11101111（对一个正数的原码取反加一就可以得到这个正数对应负数的补码。例如8位存储，十进制正数4，其二进制：00000100，取反：11111011，再加一：11111100，为 10000100（-4）的补码）

补码的最大优点是可以在加法或减法运算中，不需因为数字的正负而使用不同的计算方式。在计算机系统中，数值一律使用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统一处理；与此同时，加法和减法也可以统一处理。

使用原码运算存在的问题：
对于一个简单的加减法运算示例：1 - 1 = 0，如果转换成二进制（假设使用8位存储），-1的二进制为10000001，1的二进制为00000001，使用原码计算得 1 - 1 = -1 + 1 = 10000001 + 00000001 = 10000010 = -2，结果错误，所以符号位不能直接参与数的运算；另一方面，0这个数出现了两种表现形式：00000000和10000000（分别为+0和-0），这没有什么意义。为了解决问题，提出了补码的概念。

强制类型转换将数据范围大的数转换为数据范围小的数存在的问题：
对于Java中的基本数据类型举例，将一个int类型的整数强制类型转换为byte，可能会造成精度缺失，例如130（int）在系统中表示为 00000000 00000000 00000000 10000010，将130强转为byte，即执行此操作：(byte)130，由于byte类型只能存储8位，所以结果只剩下低8位：10000010，而最高位表示符号位，变成了一个负数。按照进制转换规则求解：首先要明确这个二进制数为补码形式，需要转换为对应的原码才为最后的结果，10000010(补码) -> 10000001(反码) -> 11111110(原码)，对应十进制数为：-126（最终结果），故执行以下命令控制台输出的数为-126。

System.out.println((byte) 130); // -126

一个8位的二进制数，暂时不考虑符号位，其能表示的最大的值为 11111111(255)，如果在上述值的基础上加1，按照逢二进一的原则，则成了 1 00000000，由于最多存储8位，所以结果成了 00000000，如果再加1，就成了00000001，依次类推。所以在8位存储的背景下，如果从0开始一直不停的往上加1，其过程就会是这种形式：0, 1, 2, …, 255, 0, 1, 2, …255, 0, 1…，一直重复循环，类似取模运算。参照以上示例（无符号数），其能表示的最大的数为255，如果再加1，最高位被丢弃，回到了0，所以其模为2^8=256，于是将模的概念运用到二进制的运算中来，具体就是运用补数。由原码运算存在问题的例子，1 - 1可以看做是 1 + (1的补数)，而1的补数=256-1=255即二进制形式的 11111111，所以 1 - 1 = 00000001 + 11111111 = 1 00000000，最高位丢弃，结果为 00000000 = 0，结果正确。这里使用了 11111111 表示 -1，即为 -1（10000001）的补码。所以负数的补码，可以看做是其对应的正数在当前模(n位，其模为2^n)下的补数(二进制形式)。

一个8位二进制正数的补码范围为 00000001~01111111（1~127），负数的补码范围（可通过对应正数的原码取反加一求得）为 10000001~11111111（-127~-1），再加上 00000000，所以能表示的范围为 10000001 ~ 01111111(-127~127)。但是上述范围少了 10000000，对于 10000000，-127 - 1 从数学的角度等于 -128，从8位二进制的角度考虑，-127 -1 = 10000001(-127的补码)+11111111(-1的补码)= 1 10000000需要舍弃最高位，最终得到10000000。所以可以将 10000000表示为-128，这样还同时解决了 +0 和 -0 的问题，保证了数据的完整性，运算逻辑也没有问题。故执行以下命令控制台输出的数为 -128。

System.out.println((byte)-127 + (byte)-1); // -128
System.out.println((byte) (127+1)); // -128

“相对补数计算”的时候不看符号，举例：
1) 8 - 6 = 8 + (-6)
ㅤㅤ0000 1000 （8）+
ㅤㅤ1111 1010 （-6）
——————————
1 ㅤ0000 0010 （2）

2) 6 - 8 = 6 + (-8)
ㅤㅤ0000 0110 （6）+
ㅤㅤ1111 1000 （-8）
——————————
ㅤㅤ1111 1110 （-2）
解释：
1) 第一位为符号位，111 1010为122（6的补数），122（6的补数）+8=130，超过128（模数）（超过128则表示减去的数相对于被减的数过小，即减去的数过小其补数则较大加上被减的数其值一定会超过128，对于被减数（为负）符号位第7位已经为1，代表128，再加上超过一个128的数第7位一定变为0，则会使结果的符号位为正），故其结果为0000 0010。（结果本来为130，超过128，多余8位的数自动被舍去，相当于对128取模则最终结果为2）
2) 第一位为符号位，111 1000为120（8的补数），120（8的补数）+6=126，未超过128（模数）（减去的数相对于被减的数过大，即减去的数过大其补数则较小加上被减的数其值不会超过128，对于被减数（为负）符号位第7位已经为1，代表128，加上的数未超过128则第7位还为1，结果的符号仍为负），故其结果为1111 1110。（结果本来为126，未超过128则还为补数，求其原来表示的数为2，即2的补数为126，故最终结果为-2）

Ⅲ Java Bitwise Operation Java位运算

Java 提供的位运算符有：左移( « )、右移( » ) 、无符号右移( >>> ) 、位与( & ) 、位或( | )、位非( ~ )、位异或( ^ )，除了位非( ~ )是一元操作符外，其它的都为二元操作符。

1) 左移 ( « )
将 5 左移 2 位，运行结果为 20

System.out.println(5 << 2); // 20

解释：
0000 0000 0000 0000 0000 0000 0000 0101 左移2位，低位补0 （5）
0000 0000 0000 0000 0000 0000 0001 0100 （20）

2) 右移( » )
将 5 右移 2 位，运行结果为 1

System.out.println(5 >> 2); // 1

解释：
0000 0000 0000 0000 0000 0000 0000 0101 右移2位，高位补0 （5）
0000 0000 0000 0000 0000 0000 0000 0001 （1）

3) 无符号右移( >>> )
将 5 右移3位，-5 分别右移 3 位和无符号右移 3 位，运行结果为0，-1 和 536870911

System.out.println(5 >> 3); // 0
System.out.println(-5 >> 3); // -1
System.out.println(-5 >>> 3); // 536870911

解释：
0000 0000 0000 0000 0000 0000 0000 0101 右移3位，高位补0 （-5）
0000 0000 0000 0000 0000 0000 0000 0000 （0）
1111 1111 1111 1111 1111 1111 1111 1011 右移3位，高位补1 （-5）
1111 1111 1111 1111 1111 1111 1111 1111 （-1）
1111 1111 1111 1111 1111 1111 1111 1011 无符号右移3位，高位补0 （-5）
0001 1111 1111 1111 1111 1111 1111 1111 （536870911）

结论：
正数右移，高位用0补，负数右移，高位用1补，当负数使用无符号右移时，高位用0补。正数或者负数左移，低位都是用0补。不存在 <<< 运算符。

4) 位与( & )
5 & 3，结果为1

System.out.println(5 & 3); // 1

解释：
0000 0000 0000 0000 0000 0000 0000 0101 （5）
0000 0000 0000 0000 0000 0000 0000 0011 （3）
———————————————————————
0000 0000 0000 0000 0000 0000 0000 0001 （1）
第一个操作数的的第n位于第二个操作数的第n位如果都是1，那么结果的第n为也为1，否则为0

5) 位或( | )
5 | 3，结果为7

System.out.println(5 | 3); // 7

解释：
0000 0000 0000 0000 0000 0000 0000 0101 （5）
0000 0000 0000 0000 0000 0000 0000 0011 （3）
———————————————————————
0000 0000 0000 0000 0000 0000 0000 0111 （7）
第一个操作数的第n位于第二个操作数的第n位只要有一个是1，那么结果的第n为也为1，否则为0

6) 位非( ~ )
~ 5，结果为-6

System.out.println(~ 5); // -6

解释：
0000 0000 0000 0000 0000 0000 0000 0101 （5）
———————————————————————
1111 1111 1111 1111 1111 1111 1111 1010 （-6）
操作数的第n位为1，那么结果的第n位为0，操作数的第n位为0，那么结果的第n位为1

7) 位异或( ^ )
5 ^ 3，结果为6

System.out.println(5 ^ 3); // 6

解释：
0000 0000 0000 0000 0000 0000 0000 0101 （5）
0000 0000 0000 0000 0000 0000 0000 0011 （3）
———————————————————————
0000 0000 0000 0000 0000 0000 0000 0110 （6）
第一个操作数的第n位于第二个操作数的第n位相反，那么结果的第n为也为1，否则为0

8) 由位运算操作符衍生而来的赋值运算符
ㅤㅤ&= ㅤ按位与赋值
ㅤㅤ|= ㅤ 按位或赋值
ㅤㅤ^= ㅤ 按位异或赋值
ㅤㅤ»=ㅤ右移赋值
ㅤㅤ>>>= 无符号右移赋值
ㅤㅤ«=ㅤ左移赋值

示例：int a = 5; a &= 3; 结果为1

int a = 5;
System.out.println(a &= 3); // 1

Ⅳ Java Operator Precedence Java运算符的优先级

Ⅴ Application 应用

1. Middle Value of Integer 整数的中间值

使用右移( » )位运算符，可以获得一个整数的1/2值：
5 » 1 = 2 向下取整
0000 0000 0000 0000 0000 0000 0000 0101 （5）
0000 0000 0000 0000 0000 0000 0000 0010 （2）
5 + 1 » 1 = 3 向上取整
0000 0000 0000 0000 0000 0000 0000 0110 （5）
0000 0000 0000 0000 0000 0000 0000 0011 （3）
解释：
对于整数 i = x * 2^2 + y * 2^1 + z * 2^0（x, y, z为0或1，表示二进制数第n位的值），右移 1 位后，相当于整数 i = x * 2^1 + y * 2^0 = (x * 2^2 + y * 2^1 + z * 2^0) / 2，即相对于原来的数除以了2（最低位舍去，舍去的值为0或者1，则对于奇数存在向上取整及向下取整的概念），当向上取整（原数+1）的原数为偶数也不影响其原本的正确结果。

应用：结合位运算求中间值的思路解决二分查找的相关问题。例如：
34. Find First and Last Position of Element in Sorted Arrayㅤㅤ在排序数组中查找元素的第一个和最后一个位置

2. Properties of Exclusive Or 异或运算的性质

1) 任何数和 0 做异或运算结果仍然是原来的数
ㅤㅤa ⊕ 0 = a
2) 任何数和其自身做异或运算结果是 0
ㅤㅤa ⊕ a = 0
3) 满足交换律和结合律
ㅤㅤa ⊕ b ⊕ a = b ⊕ a ⊕ a = b ⊕ (a ⊕ a) = b ⊕ 0 = b
证明：
将异或运算看做 加法运算后再对2求余：
ㅤㅤ1 eor 1 = (1 + 1) % 2 = 2 % 2 = 0
ㅤㅤ0 eor 0 = (0 + 0) % 2 = 0 % 2 = 0
ㅤㅤ0 eor 1 = (0 + 1) % 2 = 1 % 2 = 1
ㅤㅤ1 eor 0 = (1 + 0) % 2 = 1 % 2 = 1
异或运算（eor）的最后结果等于所有的运算数按照原来的优先级加起来再对2求余，因为加法运算本身是可交换可结合的，所以间接证明了异或运算（eor）也是可交换可结合的。

应用：结合异或运算的性质求解除了某个元素只出现一次以外其余每个元素均出现两次的非空整数数组中那个只出现了一次的元素。例如：
136. Single Numberㅤㅤ只出现一次的数字
461. Hamming Distanceㅤㅤ汉明距离
剑指 Offer 15. 二进制中1的个数ㅤㅤ二进制中1的个数
剑指 Offer 16. 数值的整数次方ㅤㅤ数值的整数次方
剑指 Offer 56 - I. 数组中数字出现的次数ㅤㅤ数组中数字出现的次数
剑指 Offer 56 - II. 数组中数字出现的次数 IIㅤㅤ数组中数字出现的次数 II

3. Count 2^n 计算2的n次方

1 << n = 2^n，对于1左移n位后的二进制数表达，只有第n位上为1其余位上都为0，故其值为2^n。

应用：使用左移运算简化（加快）2的n次方计算。例如：
222. Count Complete Tree Nodesㅤㅤ完全二叉树的节点个数

4. Count Number of 1 Bits 计算位1的个数

对于一个整数 n，计算该数二进制表示中 1 的个数。对于 n & (n - 1) ，其运算结果恰为把 n 的二进制中最低位的 1 变为 0 之后的结果。只要每次执行这个操作，就会消除掉 n 的二进制中最后一个出现的 1。因此执行 n & (n - 1) 使得 n 变成 0 的操作次数，就是 n 的二进制中 1 的个数。对于负数也适用。

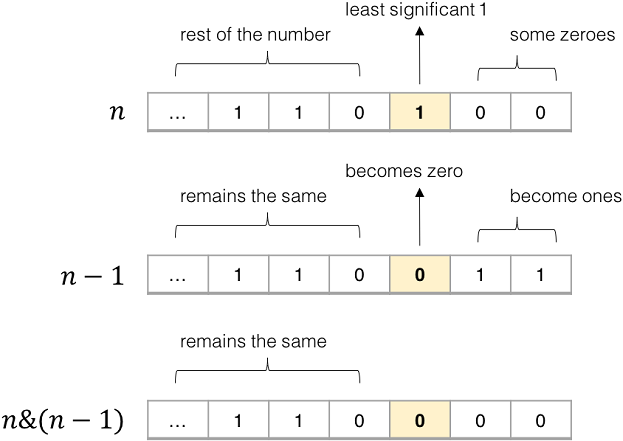
应用：计算整数 n 二进制表示中1的个数。例如：
191. Number of 1 Bitsㅤㅤ位1的个数
231. Power of Twoㅤㅤ2 的幂
剑指 Offer 15. 二进制中1的个数ㅤㅤ二进制中1的个数