数组结构以及字符串-相关算法
本博客所有文章采用的授权方式为 自由转载-非商用-非衍生-保持署名 ,转载请务必注明出处,谢谢。
博客地址:VegaLau 的博客;
微信公众号:aurusr;
内容系本人学习、研究和总结,如有雷同,实属荣幸!如有错误,欢迎通过以上联系方式指正。
introduction
抽出LeetCode题库中数组结构以及字符串相关的算法题目,再以相似类型的题目进行分类归纳总结题解。
并非每道题目的解法都是它的最优写法,只是在尽量保证代码执行高效性的前提下,为了归纳总结便于记忆而给定的解法,故这里每道题的题解也都只列出了一种写法。
Ⅰ Two Pointers 双指针
使用双指针的思路。快慢指针:指针k(慢指针)用于替换元素,指针i(快指针)用于遍历序列。定义两个指针 slow 和 fast 分别为慢指针和快指针,其中慢指针表示处理出的数组的长度,快指针表示已经检查过的数组的长度,即 nums[fast] 表示待检查的第一个元素,nums[slow−1] 或 nums[slow] 为上一个应该被保留的元素所移动到的指定位置。对撞指针:两个指针 left 和 right 初始位于序列两端。
时间复杂度:O(n) n - 序列长度
空间复杂度:O(1) 没有创建新的序列,只需要常数空间存放若干变量
283. Move Zeroes 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
示例:
输入:[0,1,0,3,12]
输出:[1,3,12,0,0]
题解:
class Solution {
public void moveZeroes(int[] nums) {
int k = 0; // nums数组中[0, ..., k)的元素均为非0元素
for (int i = 0; i < nums.length; i++) {
if (nums[i] != 0) {
if (i == k) { // 用于优化数组前几个元素都为非0的情况
k++;
} else {
nums[k++] = nums[i];
nums[i] = 0;
}
}
}
}
}
tips:
- i是否等于k的判断要写在判断当前元素是否不为0之后,否则每次进入循环体i总等于k;
- 对于i不等于k的情况,就不需要交换i和k索引处元素,直接将k处元素赋值i处元素的值并将i处元素置0即可。
27. Remove Element 移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。元素的顺序可以改变,你不需要考虑数组中超出新长度后面的元素。
示例:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
题解:
class Solution {
public int removeElement(int[] nums, int val) {
int k = 0; // nums数组中[0, ..., k)的元素均为非val元素
for (int i = 0; i < nums.length; i++) {
if (nums[i] != val) {
if (k == i) { // 用于优化数组前几个元素都为非val的情况
k++;
} else {
nums[k++] = nums[i];
}
}
}
return k;
}
}
26. Remove Duplicates from Sorted Array 删除有序数组中的重复项
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素只出现一次,返回删除后数组的新长度。不需要考虑数组中超出新长度后面的元素。
示例:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
题解:
class Solution {
public int removeDuplicates(int[] nums) {
int k = 0; // nums数组中[0, ..., k]的元素均为非重复元素
for (int i = 1; i < nums.length; i++) {
if (nums[k] != nums[i]) { // nums已按升序排列,双指针指向的元素值不同时k就需要递增
if (i - k > 1) { // 用于优化数组前几个元素都不重复的情况,防止自身给自身赋值
nums[++k] = nums[i];
} else {
k++;
}
}
}
return k + 1;
}
}
tips:
- 这里思路需要转换一下,遍历从索引1开始。
80. Remove Duplicates from Sorted Array II 删除有序数组中的重复项 II
给你一个有序数组 nums ,请你 原地 删除重复出现的元素,使每个元素最多出现两次,返回删除后数组的新长度。不需要考虑数组中超出新长度后面的元素。
示例:
输入:nums = [0,0,1,1,1,1,2,3,3]
输出:7, nums = [0,0,1,1,2,3,3]
思路:
因为相同元素最多出现两次而非一次,所以需要检查上上个应该被保留的元素nums[slow−2] 是否和当前待检查元素 nums[fast] 相同。当且仅当 nums[slow - 2] = nums[fast] 时,当前待检查元素 nums[fast] 不应该被保留(因为此时必然有 nums[slow - 2] = nums[slow - 1] = nums[fast])。
题解:
class Solution {
public int removeDuplicates(int[] nums) {
if (nums.length <= 2) return nums.length;
int k = 2; // nums数组中[0, ..., k)的元素中重复元素最多出现两次
for (int i = 2; i < nums.length; i++) {
if (nums[k - 2] != nums[i]){
nums[k++] = nums[i];
}
}
return k;
}
}
tips:
- 这里思路需要转换一下,快慢指针都从索引2开始;
- 数组的前两个数必然可以被保留,因此对于长度不超过 2 的数组无需进行任何处理。
88. Merge Sorted Array 合并两个有序数组
给你两个有序整数数组 nums1 和 nums2,请你将 nums2 合并到 nums1 中,使 nums1 成为一个有序数组。初始化 nums1 和 nums2 的元素数量分别为 m 和 n 。你可以假设 nums1 的空间大小等于 m + n,这样它就有足够的空间保存来自 nums2 的元素。
示例:
输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出:[1,2,2,3,5,6]
思路:
逆向双指针。nums1 的后半部分是空的,可以直接覆盖而不会影响结果。因此可以指针设置为从后向前遍历,每次取两者之中的较大者放进 nums1 的最后面。
题解:
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int i = m - 1; // 指向nums1数组的最后一个元素
int j = n - 1; // 指向nums2数组的最后一个元素
int tail = m + n - 1; // 指向合并后数组的最后一个元素
while (j >= 0) nums1[tail--] = i >=0 && nums1[i] > nums2[j] ? nums1[i--] : nums2[j--];
}
}
tips:
- 这里思路需要转换一下,指针都从末尾开始;
- i是否大于0判断要位于两指针元素大小比较的前面,防止空指针异常;
- i和j指针指向的位置即为nums1和nums2数组中下一个该“放置”的元素。
- 时间复杂度:O(m + n)
- 空间复杂度:O(1)
977. Squares of a Sorted Array 有序数组的平方
给你一个按非递减顺序排序的整数数组 nums,返回每个数字的平方组成的新数组,要求也按非递减顺序排序。
示例:
输入:nums = [-7,-3,2,3,11]
输出:[4,9,9,49,121]
题解:
class Solution {
public int[] sortedSquares(int[] nums) {
int i = 0;
int j = nums.length - 1;
int[] nums2 = new int[nums.length];
int tail = nums.length -1;
while(tail >= 0) {
int iVal = nums[i] * nums[i];
int jVal = nums[j] * nums[j];
if (iVal > jVal) {
nums2[tail--] = iVal;
i++;
} else {
nums2[tail--] = jVal;
j--;
}
}
return nums2;
}
}
tips:
- 这道题使用了88题合并两个有序数组的思路;
- 数组的题目首先考虑尽量低的时间复杂度,然后考虑空间复杂度,不一定所有题目都要时间复杂度O(n),空间复杂度O(1)。
- 时间复杂度:O(n)
- 空间复杂度:O(n),需要存储答案数组,所以空间复杂度为O(n)。
167. Two Sum II - Input array is sorted 两数之和 II - 输入有序数组
给定一个已按照 升序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数,你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例:
输入:numbers = [2,3,4], target = 6
输出:[1,3]
思路:
初始时两个指针分别指向第一个元素位置和最后一个元素的位置。如果两个元素之和等于目标值则发现了唯一解。如果两个元素之和小于目标值,则将左侧指针右移一位,因为最小的数与最大的数相加都小于目标值,如果左侧指针不向右移动,则当前这个第一个元素与任何其他小于最大数的数相加都会小于目标值,所以左侧指针需要右移;如果两个元素之和大于目标值,则将右侧指针左移一位,因为最小的数与最大的数相加都大于目标值,如果右侧指针不向左移动,则当前这个第二个元素与任何其他大于最小数的数相加都会大于目标值,所以右侧指针需要左移。
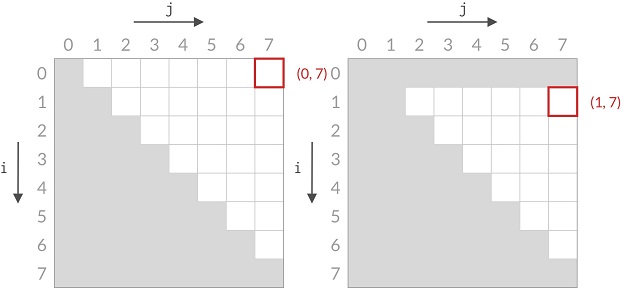
题解:
class Solution {
public int[] twoSum(int[] numbers, int target) {
for (int i = 0, j = numbers.length - 1; i < j;) {
int sum = numbers[i] + numbers[j];
if (sum == target) {
return new int[] {i + 1, j + 1};
} else if (sum > target) {
j--;
} else {
i++;
}
}
return new int[] {-1, -1}; // 防止编译报错
}
}
11. Container With Most Water 盛最多水的容器
给你 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
示例:
输入:[1,8,6,2,5,4,8,3,7]
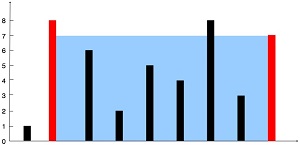
输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
思路:
设每一状态下水槽面积为 S(i,j),(0 <= i < j < n),由于水槽的实际高度由两板中的短板决定,则可得面积公式 S(i, j) = min(h[i], h[j]) × (j - i)。在每一个状态下,无论长板或短板收窄 1 格,都会导致水槽底边宽度 -1:若向内移动短板,水槽的短板 min(h[i], h[j]) 可能变大,因此水槽面积 S(i, j) 可能增大;若向内移动长板,水槽的短板 min(h[i], h[j]) 不变或变小,下个水槽的面积一定小于当前水槽面积。
题解:
class Solution {
public int maxArea(int[] height) {
int ans = 0;
for (int i = 0, j = height.length - 1; i < j;) {
ans = Math.max(Math.min(height[i], height[j]) * (j - i), ans);
if (height[i] < height[j]) {
i++;
} else {
j--;
}
}
return ans;
}
}
tips:
- 此题与167题思路相同。
240. Search a 2D Matrix II 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:每行的元素从左到右升序排列。每列的元素从上到下升序排列。
示例:
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
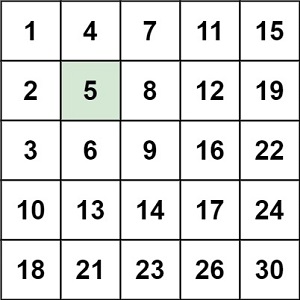
输出:true
题解:
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int m = matrix.length;
int n = matrix[0].length;
for (int i = 0, j = n - 1; i < m && j >= 0;) {
if (matrix[i][j] == target) {
return true;
} else if (matrix[i][j] < target) {
i++;
} else {
j--;
}
}
return false;
}
}
tips:
- 此题与167题思路相同。
- 时间复杂度:O(m + n)
- 空间复杂度:O(1)
16. 3Sum Closest 最接近的三数之和
给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数,使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。
示例:
输入:nums = [-1,2,1,-4], target = 1
输出:2
解释:与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
思路:
对数组调用Java的库函数java.util.Arrays类中的static void sort(int[] a) 方法,对指定的 int 型数组按数字升序进行排序。首先考虑枚举第一个元素 a,然后考虑剩下的两个元素 b 和 c,使用两重循环来枚举所有的可能情况。遍历数组,每遍历一个数组中的元素i,其固定为第一个元素a,为了防止重复枚举,在位置 [i+1, n) 的范围内枚举 b 和 c,使用左指针 left 指向 i+1 处,右指针 right 指向 nums.length-1 处,分别代表元素b和元素c,根据 sum = nums[i] + nums[left] + nums[right] 的结果,判断 sum 与目标 target 的距离,如果更近则更新结果 ans,当ans == target时则直接返回结果,同时判断 sum 与 target 的大小关系,因为数组有序,如果 sum > target 则 right–,如果 sum < target 则 left++。
题解:
class Solution {
public int threeSumClosest(int[] nums, int target) {
Arrays.sort(nums);
int len = nums.length;
int result = nums[0] + nums[1] + nums[2]; // 不能初始化为Integer.MAX_VALUE,target可能为负
for (int i = 0; i < len - 2; i++) {
int left = i + 1;
int right = len - 1;
while (left < right) {
int sum = nums[i] + nums[left] + nums[right];
if (result == target) return result;
if (Math.abs(sum - target) < Math.abs(result - target)) result = sum;
if (sum > target) {
right--;
} else {
left++;
}
}
}
return result;
}
}
tips:
- 此题与167题思路相似;
- 时间复杂度:快速排序O(nlogn) + 双层循环(固定a元素n次,双指针n次)O(n^2) = O(n^2);
- 空间复杂度:O(nlogn)
18. 4Sum 四数之和
给定一个包含 n 个整数的数组 nums 和一个目标值 target,判断 nums 中是否存在四个元素 a,b,c 和 d ,使得 a + b + c + d 的值与 target 相等?找出所有满足条件且不重复的四元组。答案中不可以包含重复的四元组。
示例:
输入:nums = [1,0,-1,0,-2,2], target = 0
输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]
思路:
先调用库函数对数组进行升序排序。三重循环,并且在循环过程中遵循以下两点:每一种循环枚举到的下标必须大于上一重循环枚举到的下标;同一重循环中,如果当前元素与上一个元素相同,则跳过当前元素。首先考虑枚举第一个元素 a,然后以同样的方式枚举第二个元素b,最后使用双指针索引考虑剩下的两个元素 c 和 d。在前两重循环中,还可以进行一些剪枝操作:在确定第一个数a之后,如果 nums[i] + nums[i+1] + nums[i+2] + nums[i+3] > target,说明此时剩下的三个数无论取什么值,四数之和一定大于 target,因此退出第一重循环(break);在确定第一个数a之后,如果 nums[i] + nums[n−3] + nums[n−2] + nums[n−1] < target,说明此时剩下的三个数无论取什么值,四数之和一定小于 target,因此第一重循环直接进入下一轮(continue),枚举 nums[i+1];在确定前两个数a和b之后,如果 nums[i] + nums[j] + nums[j+1] + nums[j+2] > target,说明此时剩下的两个数无论取什么值,四数之和一定大于 target,因此退出第二重循环(break);在确定前两个数a和b之后,如果 nums[i] + nums[j] + nums[n−2] + nums[n−1] < target,说明此时剩下的两个数无论取什么值,四数之和一定小于 target,因此第二重循环直接进入下一轮(continue),枚举 nums[j+1]。使用两重循环分别枚举前两个数a和b后,然后在两重循环枚举到的数之后使用双指针枚举剩下的两个数c和d。假设两重循环枚举到的前两个数分别位于下标 i 和 j,其中 i<j。初始时,左右指针分别指向下标 j+1 和下标 n−1。每次计算四个数的和,并进行如下操作:如果和等于 target,则将枚举到的四个数加到答案中,然后将左指针右移直到遇到不同的数,将右指针左移直到遇到不同的数(左右指针都要移动,因为left++后,sum必大于target,则需right–);如果和小于 target,则将左指针右移一位;如果和大于 target,则将右指针左移一位。
题解:
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> result = new ArrayList<>();
if (nums.length < 4) return result;
Arrays.sort(nums);
int len = nums.length;
for (int i = 0; i < len - 3; i++) {
if (i > 0 && nums[i] == nums[i - 1]) continue;
if (nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) break;
if (nums[i] + nums[len - 1] + nums[len - 2] + nums[len - 3] < target) continue;
for (int j = i + 1; j < len - 2; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
if (nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) break;
if (nums[i] + nums[j] + nums[len - 1] + nums[len - 2] < target) continue;
int left = j + 1;
int right = len - 1;
while (left < right) {
int sum = nums[i] + nums[j] + nums[left] + nums[right];
if (sum == target) {
List<Integer> ele = new ArrayList<>();
ele.add(nums[i]);
ele.add(nums[j]);
ele.add(nums[left]);
ele.add(nums[right]);
result.add(ele);
while (left < right && nums[left + 1] == nums[left]) left++;
left++;
while (left < right && nums[right - 1] == nums[right]) right--;
right--;
} else if (sum < target) {
left++; // 无需判断是否可能会重复left的值,因为sum != target时不用添加到结果中
} else {
right--; // 无需判断是否可能会重复right的值,因为sum != target时不用添加到结果中
}
}
}
}
return result;
}
}
tips:
- 此题与16题思路相似;
- 当sum == target时,为防止重复添加相同的四元组到结果中,需要判断下一位left或right是否与上一位相等,与此同时left指针与right指针都不能越界;
- 时间复杂度:快速排序O(nlogn) + 三重循环O(n^3) = O(n^3);
- 空间复杂度:忽略存储答案的空间,O(nlogn)
15. 3Sum 三数之和
给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?请你找出所有和为 0 且不重复的三元组。答案中不可以包含重复的三元组。
示例:
输入:nums = [-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
题解:
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
int len = nums.length;
if (len < 3) return result;
Arrays.sort(nums);
for (int i = 0; i < len - 2; i++) {
if (i > 0 && nums[i] == nums[i - 1]) continue;
if (nums[i] + nums[i + 1] + nums[i + 2] > 0) break;
if (nums[i] + nums[len -1] + nums[len - 2] < 0) continue;
int left = i + 1;
int right = len - 1;
while (left < right) {
int sum = nums[i] + nums[left] + nums[right];
if (sum == 0) {
List<Integer> ele = new ArrayList<>();
ele.add(nums[i]);
ele.add(nums[left]);
ele.add(nums[right]);
result.add(ele);
while (left < right && nums[left + 1] == nums[left]) left++;
left++;
while (left < right && nums[right - 1] == nums[right]) right--;
right--;
} else if (sum < 0) {
left++;
} else {
right--;
}
}
}
return result;
}
}
tips:
- 此题与18题思路相同;
- 时间复杂度:快速排序O(nlogn) + 两重循环O(n^2) = O(n^2);
- 空间复杂度:忽略存储答案的空间,O(nlogn)
Ⅱ Two Pointers - String 双指针 - 字符串
使用双指针思路的字符串的相关题目。
时间复杂度:O(n) n - 字符串 s 的长度
空间复杂度:O(1)或者O(n) 需要新建长度为n的数组存储字符串转换成的字符数组时空间复杂度为O(n)。
125. Valid Palindrome 验证回文串
给定一个字符串,验证它是否是回文串,只考虑字母和数字字符,可以忽略字母的大小写。空字符串为有效的回文串。
示例:
输入:”A man, a plan, a canal: Panama”
输出:true
题解:
class Solution {
public boolean isPalindrome(String s) {
int left = 0, right = s.length() - 1;
while (left < right) {
while (left < right && !Character.isLetterOrDigit(s.charAt(left))) left++;
while (left < right && !Character.isLetterOrDigit(s.charAt(right))) right--;
if (left < right) {
if (Character.toLowerCase(s.charAt(left)) != Character.toLowerCase(s.charAt(right))) return false;
left++;
right--;
}
}
return true;
}
}
tips:
- 对JDK API中java.lang.Character类及java.lang.String类的熟悉。
344. Reverse String 反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。你必须原地修改输入数组。你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例:
输入:[“h”,”e”,”l”,”l”,”o”]
输出:[“o”,”l”,”l”,”e”,”h”]
题解:
class Solution {
public void reverseString(char[] s) {
int left = 0, right = s.length - 1;
while (left < right) swap(s, left++, right--);
}
private void swap(char[] array, int i, int j) {
char temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
345. Reverse Vowels of a String 反转字符串中的元音字母
编写一个函数,以字符串作为输入,反转该字符串中的元音字母。
示例:
输入:”leetcode”
输出:”leotcede”
题解:
class Solution {
public String reverseVowels(String s) {
char[] sArray = s.toCharArray();
int left = 0, right = sArray.length - 1;
while (left < right) {
while (left < right && !isVowel(sArray, left)) left++;
while (left < right && !isVowel(sArray, right)) right--;
if (left < right) swap(sArray, left++, right--);
}
return String.valueOf(sArray);
}
private void swap(char[] array, int i, int j) {
char temp = array[i];
array[i] = array[j];
array[j] = temp;
}
private boolean isVowel(char[] array, int index) {
if (array[index] == 'a' || array[index] == 'e' || array[index] == 'i' || array[index] == 'o' || array[index] == 'u' || array[index] == 'A' || array[index] == 'E' || array[index] == 'I' || array[index] == 'O' || array[index] == 'U') return true;
return false;
}
}
tips:
- 使用方法封装一部分功能(比如条件判断)很重要;
- char类型在运算的时候会被首先提升为int类型然后再计算;
- 对JDK API中java.lang.String类的熟悉。
680. Valid Palindrome II 验证回文字符串 Ⅱ
给定一个非空字符串 s,最多删除一个字符。判断是否能成为回文字符串。字符串只包含从 a-z 的小写字母。
示例:
输入:”abca”
输出:true
题解:
class Solution {
public boolean validPalindrome(String s) {
int left = 0, right = s.length() - 1;
left = isValidPalindrome(s, left, right);
if (left == -1) {
return true;
} else {
right = s.length() - 1 - left;
if (isValidPalindrome(s, left + 1, right) == -1 || isValidPalindrome(s, left, right - 1) == -1) return true;
}
return false;
}
// 判断子字符串是否为回文串的方法
private int isValidPalindrome(String s, int left, int right) {
while (left < right) {
if (s.charAt(left) == s.charAt(right)) {
left++;
right--;
} else {
return left; // 当前子串不是回文字符串时返回第一个不符合回文条件的left索引
}
}
return -1; // 当前子串是回文字符串时返回-1
}
}
tips:
- 使用方法封装一部分功能(比如条件判断)很重要,在此题中如果不将判断一个子串是否为回文串封装为一个方法,将其判断写在方法内部则会使代码逻辑冗赘。
541. Reverse String II 反转字符串 II
给定一个字符串 s 和一个整数 k,你需要对从字符串开头算起的每隔 2k 个字符的前 k 个字符进行反转。如果剩余字符少于 k 个,则将剩余字符全部反转。如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
示例:
输入:s = “abcdefg”, k = 2
输出:”bacdfeg”
题解:
class Solution {
public String reverseStr(String s, int k) {
char[] sArray = s.toCharArray();
int left = 0;
int right = 0; // 初始化,防止写在循环内部导致重复定义
while (left < sArray.length) {
// 剩余字符少于k个将剩余字符全部反转,剩余字符大于或等于k个反转前k个字符
right = sArray.length - left < k ? sArray.length - 1 : left + k - 1;
swap(sArray, left, right);
left += 2 * k;
}
return String.valueOf(sArray);
}
private void swap(char[] array, int left, int right) {
while (left < right) {
char temp = array[left];
array[left++] = array[right];
array[right--] = temp;
}
}
}
tips:
- 当然并非所有题目都要优先考虑将一部分功能(比如条件判断、数组元素交换等)用方法封装起来,相比680题,在此题中可以将条件判断、数组元素交换各封装为一个方法,但必要性不大,完全可以清晰地写在原方法中;
- 判断时只需要使用子串起始索引left就可以,不需要再附加终止索引right的判断。
557. Reverse Words in a String III 反转字符串中的单词 III
给定一个字符串,你需要反转字符串中每个单词的字符顺序,同时仍保留空格和单词的初始顺序。在字符串中,每个单词由单个空格分隔,并且字符串中不会有任何额外的空格。
示例:
输入:”Let’s take LeetCode contest”
输出:”s’teL ekat edoCteeL tsetnoc”
题解:
class Solution {
public String reverseWords(String s) {
char[] sArray = s.toCharArray();
int left = 0;
int right = 0; // 初始化,防止写在循环内部导致重复定义
while (left < sArray.length) {
right = left + 1;
while (right < sArray.length && sArray[right] != ' ') right++;
swap(sArray, left, right - 1);
left = right + 1;
}
return new String(sArray); // 使用构造方法的方式
}
private void swap(char[] array, int left, int right) {
while (left < right) {
char temp = array[left];
array[left++] = array[right];
array[right--] = temp;
}
}
}
tips:
- 与541题思路相同;
- 对于数组来说,使用[]索引取值,就需要注意是否越界问题。
Ⅲ Sliding Window 滑动窗口
使用双指针,滑动窗口的思路,定义两个指针left和right分别表示子数组(滑动窗口)的开始位置和结束位置,实现不同的功能。
时间复杂度:O(n) n - 序列长度,最坏情况左指针和右指针分别会遍历整个序列一次。
空间复杂度:O(1) 或者 O(∣Σ∣)(使用频度数组时,其中 Σ 表示字符集,即字符串中可以出现的字符,∣Σ∣ 表示字符集的大小)
209. Minimum Size Subarray Sum 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 target 。找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
思路:
定义两个指针left和right分别表示子数组(滑动窗口)的开始位置和结束位置,维护变量sum存储子数组中的元素和,左右指针包含的子数组窗口区间一直在向右滑动。此题是满足要求移动左指针寻找新的满足要求的子数组。
题解:
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int left = 0, right = -1; // nums[left, right]为滑动窗口
int sum = 0; // 滑动窗口子数组元素的和
int minLen = nums.length + 1; // 存在符合条件的子数组时minLen的值一定会被替换
while (left < nums.length) {
if (right + 1 < nums.length && sum < target) {
sum += nums[++right];
} else {
sum -= nums[left++];
}
if (sum >= target) minLen = Math.min(minLen, right - left + 1);
}
return minLen == nums.length + 1 ? 0 : minLen;
}
}
tips:
- 对于数组来说,使用[]索引取值,就需要注意是否越界问题;
- 判断时只需要使用子串起始索引left就可以,不需要再附加终止索引right的判断。
3. Longest Substring Without Repeating Characters 无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例:
输入:s = “pwwkew”
输出:3
解释:因为无重复字符的最长子串是 “wke”,所以其长度为 3。
思路:
定义两个指针left和right分别表示子数组(滑动窗口)的开始位置和结束位置。判断子串是否含有重复字符还需要使用额外的数据结构比如数组存储ASCII为数组索引值的字符在子串(滑动窗口)中出现的频率。此题是不满足要求移动左指针寻找新的满足要求的子数组。
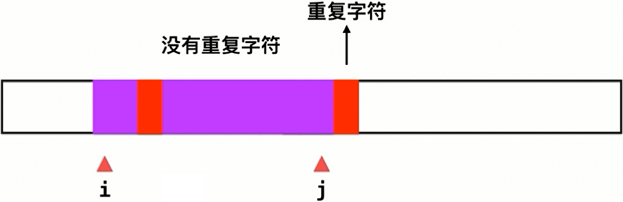
题解:
class Solution {
public int lengthOfLongestSubstring(String s) {
int[] charFreq = new int[128]; // 存储ASCII为数组索引值的字符在子串(滑动窗口)中出现的频率
int left = 0, right = -1; // nums[left, right]为滑动窗口
int maxLen = 0;
while (left < s.length()) {
if (right + 1 < s.length() && charFreq[s.charAt(right + 1)] == 0) {
charFreq[s.charAt(++right)]++;
} else {
charFreq[s.charAt(left++)]--;
}
maxLen = Math.max(maxLen, right - left + 1); // 当前子串(滑动窗口)一定不含有重复字符
}
return maxLen;
}
}
tips:
- 对于数组来说需要注意是否越界问题,同理对于字符串来说,使用charAt()方法取值也需要注意是否越界的问题;
- char类型在运算的时候会被首先提升为int类型然后再计算,适用于算术运算、比较运算、赋值运算和数组的索引赋值,此题运用了数组的索引赋值;
- 判断时只需要使用子串起始索引left就可以,不需要再附加终止索引right的判断;
- 当字符串中出现较长的相同连续字符时left与right会交替的向前移动(滑动窗口);
- 时间复杂度:O(n);
- 空间复杂度:O(∣Σ∣),此题字符集为所有 ASCII 码在 [0,128) 内的字符,即∣Σ∣=128。
424. Longest Repeating Character Replacement 替换后的最长重复字符
给你一个仅由大写英文字母组成的字符串,你可以将任意位置上的字符替换成另外的字符,总共可最多替换 k 次。在执行上述操作后,找到包含重复字母的最长子串的长度。
示例:
输入:s = “AABABBA”, k = 1
输出:4
解释:将中间的一个’A’替换为’B’,字符串变为 “AABBBBA”。子串 “BBBB” 有最长重复字母, 答案为 4。
思路:
维护一个滑动窗口,保证窗口大小减去出现次数最多字符的次数之差小于等于k即符合题意,窗口可继续扩张(left不变,right++),否则就不符合题意就滑动窗口(left++,right++)。记录子串(滑动窗口)中出现最多字符的次数还需要使用额外的数据结构比如数组存储子串每个字符出现的次数。如果找到了一个长度为 L 且替换 k 个字符以后全部相等的子串,就没有必要考虑长度小于等于 L 的子串,故在上次符合题目条件后下一个right索引右移不符合条件后,left索引右移right索引也需要右移(右移后可能不满足题目条件,但目的是找到长度大于 L 的子串,也可能一直到左右索引交替移动到数组末尾还是没有符合题意且比 L 更长的子串,但是返回值为right - left,因为是左右索引交替移动,其长度还是等于上一次符合题意的 L 长度)。子串出现次数最多字符的次数maxCount不需要维护,只需要保证频数数组符合当前子串(滑动窗口)的正确性即可(频数数组的正确性保证了下一次更新子串出现次数最多字符的次数maxCount的正确性),因为题目要求找到最长的子串,当出现更优解时自然会更新子串出现次数最多字符的次数maxCount,此时也是符合当前子串的正确性的。此题是不满足要求移动左指针寻找新的满足要求的子数组(与其他滑动窗口题目不同,左指针移动后右指针也移动)。
题解:
class Solution {
public int characterReplacement(String s, int k) {
int left = 0, right = 0;
int maxCount = 0; // 子串出现次数最多字符的次数
int[] charFreq = new int[26];
while (right < s.length()) {
maxCount = Math.max(maxCount, ++charFreq[s.charAt(right++) - 'A']);
if (right - left > maxCount + k) charFreq[s.charAt(left++) - 'A']--;
}
return right - left;
}
}
tips:
- 此题思路与3题相近,3题中当字符串中出现较长的相同连续字符时left与right会交替的向前移动(滑动窗口),此题中无更优解就会滑动窗口;
- 记录频次时减去’A’,char类型在运算的时候会被首先提升为int类型然后再计算,不需要查A对应的ASCII值;
- 判断时只需要使用子串终止索引right即可;
- 时间复杂度:O(n);
- 空间复杂度:O(∣Σ∣),此题字符集(所有大写字母 )为所有 ASCII 码在 [65, 90] 内的字符,即∣Σ∣=26。
438. Find All Anagrams in a String 找到字符串中所有字母异位词
给定一个字符串 s 和一个非空字符串 p,找到 s 中所有是 p 的字母异位词的子串,返回这些子串的起始索引。字符串只包含小写英文字母。字母异位词指字母相同,但排列不同的字符串。不考虑答案输出的顺序。
示例:
输入:s: “cbaebabacd” p: “abc”
输出:[0, 6]
解释:起始索引等于 0 的子串是 “cba”, 它是 “abc” 的字母异位词。起始索引等于 6 的子串是 “bac”, 它是 “abc” 的字母异位词。
思路:
窗口长度固定,每次向右移动一位,判断当前滑动窗口是否符合题意。
题解:
class Solution {
public List<Integer> findAnagrams(String s, String p) {
int len = p.length();
List<Integer> list = new ArrayList<>();
if (len > s.length()) return list;
int[] pFreq = new int[26];
int[] sFreq = new int[26];
int left = 0, right = len - 1;
boolean flag = true;
for (int i = 0; i < len; i++) {
pFreq[p.charAt(i) - 'a']++;
sFreq[s.charAt(i) - 'a']++;
}
while (right < s.length()) {
for (int i = 0; i < 26; i++) {
if (pFreq[i] != sFreq[i]) {
flag = false;
break;
}
}
if (flag) list.add(left);
sFreq[s.charAt(left++) - 'a']--;
if (right + 1 < s.length()) {
sFreq[s.charAt(++right) - 'a']++;
} else {
right++;
}
flag = true;
}
return list;
}
}
tips:
- 此题中判断s字符串滑动窗口中字母与p字符串中字母出现的频率是否相等,即sFreq数组与pFreq元素是否相等,还可以使用java.util.Arrays类中的static boolean equals(int[] a, int[] a2)方法,如果两个指定的 int 型数组彼此相等,则返回 true;
- 时间复杂度:O(n);
- 空间复杂度:O(∣Σ∣),除去返回答案所用集合的空间。此题字符集(所有小写字母 )为所有 ASCII 码在 [97, 122] 内的字符,即∣Σ∣=26*2=52。
567. Permutation in String 字符串的排列
给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的排列。即第一个字符串的排列之一是第二个字符串的 子串 。
示例:
输入:s1 = “ab” s2 = “eidbaooo”
输出:true
解释:s2 包含 s1 的排列之一 (“ba”)。
题解:
class Solution {
public boolean checkInclusion(String s1, String s2) {
if (s1.length() > s2.length()) return false;
int[] s1Freq = new int[26];
int[] s2Freq = new int[26];
for (int i = 0; i < s1.length(); i++) {
s1Freq[s1.charAt(i) - 'a']++;
s2Freq[s2.charAt(i) - 'a']++;
}
int left = 0, right = s1.length() - 1;
while (right < s2.length()) {
if (Arrays.equals(s1Freq, s2Freq)) return true;
s2Freq[s2.charAt(left++) - 'a']--;
if (right + 1 < s2.length()) {
s2Freq[s2.charAt(++right) - 'a']++;
} else {
right++;
}
}
return false;
}
}
tips:
- 此题思路与438题相同;
- 使用java.util.Arrays类中的static boolean equals(int[] a, int[] a2)方法来判断滑动窗口中字母与s1字符串中字母出现的频率是否相等,如果两个指定的 int 型数组彼此相等,则返回 true;
- 时间复杂度:O(n);
- 空间复杂度:O(∣Σ∣),此题字符集(所有小写字母 )为所有 ASCII 码在 [97, 122] 内的字符,即∣Σ∣=26*2=52。
76. Minimum Window Substring 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
示例:
输入:s = “ADOBECODEBANC”, t = “ABC”
输出:”BANC”
思路:
不断增加right使滑动窗口增大,直到窗口包含了字符串t的所有元素,不断增加left使滑动窗口缩小,直到碰到一个必须包含的元素,这个时候不能再left++了,记录此时滑动窗口对应的字符串和上次保存的字符串取长度更小的进行保存,故初始定义结果字符串时其长度需要大于s字符串。使left再增加一个位置,此时滑动窗口肯定不满足条件了,那么继续使得right++寻找新的满足条件的滑动窗口。此题是满足要求移动左指针寻找新的不满足要求的子数组(与其他滑动窗口题目不同,左指针移动后右指针也移动)。
题解:
class Solution {
public String minWindow(String s, String t) {
if (t.length() > s.length()) return "";
int left = 0, right = t.length() - 1;
int len = t.length();
int[] tFreq = new int[58];
int[] sFreq = new int[58];
boolean flag = true;
String result = s + "a";
for (int i = 0; i < len; i++) {
tFreq[t.charAt(i) - 'A']++;
sFreq[s.charAt(i) - 'A']++;
}
while (right < s.length()) {
for (int i = 0; i < 58; i++) {
if (tFreq[i] != 0 && tFreq[i] > sFreq[i]) {
flag = false;
break;
}
}
if (flag) {
while (sFreq[s.charAt(left) - 'A'] > tFreq[s.charAt(left) - 'A']) sFreq[s.charAt(left++) - 'A']--;
result = result.length() > right - left + 1 ? s.substring(left, right + 1) : result;
sFreq[s.charAt(left++) - 'A']--;
}
flag = true;
if (right + 1 < s.length()) {
sFreq[s.charAt(++right) - 'A']++;
} else {
right++;
}
}
return result.length() > s.length() ? "" : result;
}
}
tips:
- 此题思路与438题相近,不同的是438题中需要两个频数数组相等,此题中sFreq >= tFreq时滑动窗口满足要求,否则sFreq < tFreq时不满足要求;
- 记录频次时减去’A’,char类型在运算的时候会被首先提升为int类型然后再计算,不需要查A对应的ASCII值;
- 判断时只需要使用子串终止索引right即可;
- 时间复杂度:O(n);
- 空间复杂度:O(∣Σ∣),除去返回答案所用集合的空间。此题字符集(所有大小写字母 )为所有 ASCII 码在 [65, 122] 内的字符(不包括大小写字母之间的91~96 ASCII值的字符),即∣Σ∣=58*2=116。
992. Subarrays with K Different Integers K 个不同整数的子数组
给定一个正整数数组 A,如果 A 的某个子数组中不同整数的个数恰好为 K,则称 A 的这个连续、不一定不同的子数组为好子数组。1 <= A[i] <= A.length 。
示例:
输入:A = [1,2,1,2,3], K = 2
输出:7
解释:恰好由 2 个不同整数组成的子数组:[1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2]。
思路:
滑动窗口对应的子区间满足不同整数的个数不超过K个,一次调用方法所有不同滑动窗口新增的不同子数组的个数和即为最多存在 K 个不同整数的子区间的个数。不同滑动窗口新增的不同子数组的个数为当前不同滑动窗口的长度,即终止索引-起始索引(终止索引为开区间),也即左边界固定前提下,根据右边界最右的下标,计算出来的子区间的个数,eg:最多包含 3 种不同整数的子区间(滑动窗口) [1, 3, 2, 3] ,新增的子区间为 [3]、[2, 3]、[3, 2, 3]、[1, 3, 2, 3]。最多存在 K 个不同整数的子区间的个数与恰好存在 K 个不同整数的子区间的个数的差恰好等于最多存在 K−1 个不同整数的子区间的个数,故调用两次方法就可求解。判断子数组含有重复数字的个数还需要使用额外的数据结构比如数组存储值为数组索引值的元素在子数组(滑动窗口)中出现的频率,终止索引处的元素出现频率为0表示子数组中多了一个不同的整数,起始索引处的元素出现频率为0表示子数组中少了一个不同的整数。此题是不满足要求移动左指针寻找新的满足要求的子数组。
题解:
class Solution {
public int subarraysWithKDistinct(int[] A, int K) {
return subarraysWithMostKDistinct(A, K) - subarraysWithMostKDistinct(A, K -1);
}
// 数组中不同整数个数最多为K个的连续子数组的个数
private int subarraysWithMostKDistinct(int[] array, int k) {
int left = 0;
int right = 0; // A[left, right)为滑动窗口
int count = 0; // 滑动窗口(子数组)中不同整数的个数
int result = 0;
int[] intFreq = new int[array.length + 1]; // 存储值为数组索引值的元素在子串(滑动窗口)中出现的频率 1 <= A[i] <= A.length
while (right < array.length) {
if (intFreq[array[right]] == 0) count++;
intFreq[array[right]]++;
right++;
while (count > k) {
if (--intFreq[array[left++]] == 0) count--;
}
result += right - left; // 当前子串(滑动窗口)不同整数个数一定不超过K个
}
return result;
}
}
tips:
- 优先级:算术运算 > 比较运算 > 逻辑运算 > 赋值运算;
- 判断时只需要使用子数组终止索引right就可以;
- 时间复杂度:O(n),此题调用两次方法,最多遍历4次数组。
- 空间复杂度:O(∣Σ∣),此题正整数集为1 <= A[i] <= A.length,即∣Σ∣=A.length = n。
718. Maximum Length of Repeated Subarray 最长重复子数组
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例:
输入:A: [1,2,3,2,1],B: [3,2,1,4,7]
输出:3
解释:长度最长的公共子数组是 [3, 2, 1] 。
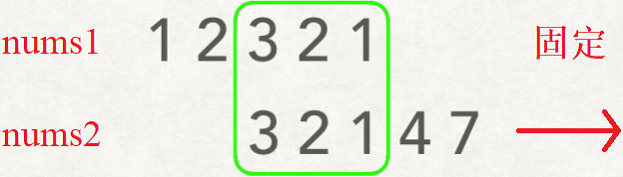
思路:
枚举 nums1 和 nums2数组 所有的对齐方式。对齐的方式有两种,一种为 nums1数组 固定,nums2数组 的首元素与 nums1数组 中的某个元素对齐;另一种为 nums2数组 不变,nums1数组 的首元素与 nums2数组 中的某个元素对齐。对于每一种对齐方式计算它们相对位置(滑动窗口)相同的重复子数组即可。此题滑动窗口是两个数组的重叠部分。
题解:
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int nums1Len = nums1.length, nums2Len= nums2.length;
int result = 0;
// nums1数组固定,向右移动nums2数组
for (int i = 0; i < nums1Len; i++) {
int traverseLen = Math.min(nums1Len - i, nums2Len);
result = Math.max(result, findWindowLength(nums1, nums2, i, 0, traverseLen));
}
// nums2数组固定,向右移动nums1数组
for (int i = 0; i < nums2Len; i++) {
int traverseLen = Math.min(nums2Len - i, nums1Len);
result = Math.max(result, findWindowLength(nums1, nums2, 0, i, traverseLen));
}
return result;
}
// 求解当前滑动窗口中最长公共子串的长度
private int findWindowLength(int[] nums1, int[] nums2, int nums1Start, int nums2Start, int traverseLen) {
int nowResult = 0, maxLen = 0;
for (int i = 0; i < traverseLen; i++) {
if (nums1[nums1Start + i] == nums2[nums2Start + i]) {
maxLen++;
} else {
maxLen = 0; // 下一个不等的元素出现时置零
}
nowResult = Math.max(nowResult, maxLen);
}
return nowResult;
}
}
tips:
- 注意最大遍历长度traverseLen的取值;
- 时间复杂度:O((N+M) * min(N,M));
- 空间复杂度:O(1)。
Ⅳ Hash Table 哈希表
使用底层实现为哈希表的Set及Map集合等的数组相关题目。哈希表(散列表)是根据关键码值(Key value)直接进行访问的数据结构。它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。哈希表插入、查找及删除的时间复杂度均为O(1)。
349. Intersection of Two Arrays 两个数组的交集
给定两个数组,编写一个函数来计算它们的交集。出结果中的每个元素一定是唯一的。可以不考虑输出结果的顺序。
示例:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
思路:
使用Set集合不包含重复元素的特性。
题解:
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
Set<Integer> nums1EleSet = new HashSet<>();
Set<Integer> intersection = new HashSet<>();
for (int i = 0; i < nums1.length; i++) {
nums1EleSet.add(nums1[i]);
}
for (int i = 0; i < nums2.length; i++) {
if (nums1EleSet.contains(nums2[i])) intersection.add(nums2[i]);
}
int[] result = new int[intersection.size()];
int i = 0;
for (Integer ele : intersection) {
result[i++] = ele;
}
return result;
}
}
tips:
- 对java.util.Set
接口类的熟悉; - 时间复杂度:O(m+n),其中 m 和 n 分别是两个数组的长度。使用两个集合分别存储两个数组中的元素需要 O(m+n) 的时间,遍历较小的集合并判断元素是否在另一个集合中需要 O(min(m,n)) 的时间,因此总时间复杂度是 O(m+n);
- 空间复杂度:O(m+n),其中 m 和 n 分别是两个数组的长度。空间复杂度主要取决于两个集合。
350. Intersection of Two Arrays II 两个数组的交集 II
给定两个数组,编写一个函数来计算它们的交集。输出结果中每个元素出现的次数,应与元素在两个数组中出现次数的最小值一致。可以不考虑输出结果的顺序。
示例:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2,2]
思路:
使用Map集合存储较短数组中每个数字出现的次数,然后遍历另一个数组,对于每个数字如果在map集合中存在这个数字,则将该数字添加到答案,并减少哈希表(map集合)中该数字出现的次数。
题解:
class Solution {
public int[] intersect(int[] nums1, int[] nums2) {
if (nums1.length > nums2.length) return intersect(nums2, nums1); // 使用最短的数组来建立Map集合
Map<Integer, Integer> nums1EleMap = new HashMap<>();
for (int i = 0; i < nums1.length; i++) {
if (!nums1EleMap.containsKey(nums1[i])) {
nums1EleMap.put(nums1[i], 1);
} else {
nums1EleMap.put(nums1[i], nums1EleMap.get(nums1[i]) + 1);
}
}
int[] result = new int[nums1.length]; // 结果数组的长度一定不会超过nums1数组元素频度map集合的大小
int len = 0; // 结果数组的有效长度
for (int i = 0; i < nums2.length; i++) {
if (nums1EleMap.containsKey(nums2[i])) {
result[len++] = nums2[i];
if (nums1EleMap.get(nums2[i]) == 1) {
nums1EleMap.remove(nums2[i]);
} else {
nums1EleMap.put(nums2[i], nums1EleMap.get(nums2[i]) - 1);
}
}
}
return Arrays.copyOf(result, len);
}
}
tips:
- 对java.util.Map<K,V>接口类的熟悉;
- 选取最短的数组采用递归的方式(最多只自己调用自己一次);
- 使用java.util.Arrays类中的static int[] copyOf(int[] original, int newLength) 方法,复制指定的数组,截取或用 0 填充(如有必要),以使副本具有指定的长度;
- 时间复杂度:O(m+n),其中 m 和 n 分别是两个数组的长度。需要遍历两个数组并对哈希表进行操作,哈希表操作的时间复杂度是 O(1),因此总时间复杂度与两个数组的长度和呈线性关系;
- 空间复杂度:O(min(m,n)),其中 m 和 n 分别是两个数组的长度。对较短的数组进行哈希表的操作,哈希表的大小不会超过较短的数组的长度。为返回值创建一个数组 result,其长度为较短数组的长度。
290. Word Pattern 单词规律
给定一种规律 pattern 和一个字符串 str ,判断 str 是否遵循相同的规律。这里的 遵循 指完全匹配,即pattern 里的每个字母和字符串 str 中的每个非空单词之间存在着双向连接的对应规律。
示例:
输入:pattern = “abba”, str = “dog dog dog dog”
输出:false
思路:
使用Map集合存储模式串字符(key)和匹配字符串中的单词(value),遍历模式串中的字符,当key存在value不相等或者key不存在map中包含值value(这个单词已经被存了,即模式串字符不同单词相同)时不符合单词规律匹配,返回false。
题解:
class Solution {
public boolean wordPattern(String pattern, String s) {
String[] strs = s.split(" ");
int ptnLen = pattern.length();
if (strs.length != ptnLen) return false;
Map<Character, String> mapping = new HashMap<>();
for (int i = 0; i < ptnLen; i++) {
char ch = pattern.charAt(i);
String str = mapping.get(ch);
if (str == null) {
if (mapping.containsValue(strs[i])) return false;
mapping.put(ch, strs[i]);
} else {
if (!str.equals(strs[i])) return false;
}
}
return true;
}
}
tips:
- 注意char类型的包装类为Character;
- 需要多次使用的由方法返回值给定的变量尽量定义在单独语句,减少时间频度(避免多次调用方法);
- 使用java.util.Map<K,V>接口类中的方法boolean containsValue(Object value) ,如果此映射将一个或多个键映射到指定值,则返回 true。 判断map中是否包含值value;
- 时间复杂度:O(n),其中 n 为 pattern 的长度;
- 空间复杂度:O(n)
205. Isomorphic Strings 同构字符串
给定两个字符串 s 和 t,判断它们是否是同构的。如果 s 中的字符可以按某种映射关系替换得到 t ,那么这两个字符串是同构的。每个出现的字符都应当映射到另一个字符,同时不改变字符的顺序。不同字符不能映射到同一个字符上,相同字符只能映射到同一个字符上,字符可以映射到自己本身。
示例:
输入:s = “paper”, t = “title”
输出:true
题解:
class Solution {
public boolean isIsomorphic(String s, String t) {
Map<Character, Character> mapping = new HashMap<>();
if (s.length() != t.length()) return false;
for (int i = 0; i < s.length(); i++) {
char sCh = s.charAt(i);
char tCh = t.charAt(i);
Character ch = mapping.get(sCh);
if (ch == null) {
if (mapping.containsValue(tCh)) return false;
mapping.put(sCh, tCh);
} else {
if (tCh != ch) return false;
}
}
return true;
}
}
tips:
- 与290题思路相同;
- Character包装类在进行与字符char比较时也可以自动拆箱;
- 时间复杂度:O(n)
- 空间复杂度:O(n)
451. Sort Characters By Frequency 根据字符出现频率排序
给定一个字符串,请将字符串里的字符按照出现的频率降序排列。’A’和’a’被认为是两种不同的字符。
示例:
输入:”tree”
输出:”eert” (”eetr”也是一个有效的答案)
思路:
使用桶排序的思路,桶数组每个索引为i的值存储出现次数为i字符集合。
题解:
class Solution {
public String frequencySort(String s) {
Map<Character, Integer> freq = new HashMap<>();
int len = s.length();
for (int i = 0; i < len; i++) {
freq.put(s.charAt(i), freq.getOrDefault(s.charAt(i), 0) + 1);
}
List<Character>[] bucket = new List[len + 1]; // 桶数组的索引表示某个字符出现的次数,最大为n次
for (Character key : freq.keySet()) {
int value = freq.get(key);
if (bucket[value] == null) bucket[value] = new ArrayList();
bucket[value].add(key);
}
StringBuffer result = new StringBuffer();
for (int i = len; i > 0; i--) {
if (bucket[i] != null) {
for (char ch : bucket[i]) {
for (int j = 0; j < i; j++) {
result.append(ch);
}
}
}
}
return result.toString();
}
}
tips:
- 任何数据类型都能作为数组当中元素的类型;
- 时间复杂度:O(n)
- 空间复杂度:O(n)
347. Top K Frequent Elements 前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按任意顺序返回答案。
示例:
输入:nums = [1,1,1,2,2,3], k = 2
输出:[1,2]
题解:
class Solution {
public int[] topKFrequent(int[] nums, int k) {
Map<Integer, Integer> freq = new HashMap<>();
int len = nums.length;
for (int i = 0; i < len; i++) {
freq.put(nums[i], freq.getOrDefault(nums[i], 0) + 1);
}
List<Integer>[] bucket = new List[len + 1];
for (int key : freq.keySet()) {
int value = freq.get(key);
if (bucket[value] == null) bucket[value] = new ArrayList();
bucket[value].add(key);
}
int count = 0; // 计数当前为出现频率第k高的元素
int[] result = new int[k];
for (int i = len; count < k; i--) {
if (bucket[i] != null) {
for (int ele : bucket[i]) {
if (count < k) {
result[count++] = ele;
} else {
break;
}
}
}
}
return result;
}
}
tips:
- 与451题思路相同;
- 时间复杂度:O(n)
- 空间复杂度:O(n)
692. Top K Frequent Words 前K个高频单词
给一非空的单词列表,返回前 k 个出现次数最多的单词。返回的答案应该按单词出现频率由高到低排序。如果不同的单词有相同出现频率,按字母顺序排序。输入的单词均由小写字母组成。
示例:
输入:[“i”, “love”, “leetcode”, “i”, “love”, “coding”], k = 2
输出:[“i”, “love”]
解释:”i” 和 “love” 为出现次数最多的两个单词,均为2次。按字母顺序 “i” 在 “love” 之前。
思路:
使用Map集合存储字符串数组中每个单词的频率,然后将其添加到大小为 k 的小顶堆中(使用java.util.PriorityQueue
题解:
class Solution {
public List<String> topKFrequent(String[] words, int k) {
Map<String, Integer> freq = new HashMap<>();
for (String word : words) {
freq.put(word, freq.getOrDefault(word, 0) + 1);
}
PriorityQueue<String> heap = new PriorityQueue<>(new Comparator<String>() {
public int compare(String s1, String s2) {
return freq.get(s1) == freq.get(s2) ? s2.compareTo(s1) : freq.get(s1) - freq.get(s2);
}
});
for (String word : freq.keySet()) {
heap.offer(word);
if (heap.size() > k) heap.poll(); // 保证优先队列只有当前“最大的”k个单词
}
List<String> result = new ArrayList<>();
for (int i = 0; i < k; i++) {
result.add(heap.poll());
}
Collections.reverse(result);
return result;
}
}
tips:
- java.util.PriorityQueue
类是一个基于优先级堆的无界优先级队列。优先级队列的元素按照其自然顺序进行排序,或者根据构造队列时提供的 Comparator 进行排序,具体取决于所使用的构造方法。优先级队列不允许使用 null 元素。依靠自然顺序的优先级队列还不允许插入不可比较的对象(可能导致 ClassCastException)。 此队列的头是按指定排序方式确定的最小元素。如果多个元素都是最小值,则头是其中一个元素(选择方法是任意的)。队列获取操作 poll、remove、peek 和 element 访问处于队列头的元素。此实现不是同步的,此实现为排队和出队方法(offer、poll、remove() 和 add)提供 O(log(n)) 时间,为 remove(Object) 和 contains(Object) 方法提供线性时间;为获取方法(peek、element 和 size)提供固定时间。此题使用PriorityQueue 类来实现小顶堆的功能; - 使用 PriorityQueue (Comparator<? super E> comparator) 创建具有默认初始容量的 PriorityQueue ,并根据指定的比较器对其元素进行排序。来实例化此优先级队列(JDK 1.8新特性);
- 使用java.lang.String类的 int compareTo(String anotherString) 方法,按字典顺序比较两个字符串(如果参数字符串等于此字符串则返回值 0,如果此字符串按字典顺序小于字符串参数则返回一个小于 0 的值,如果此字符串按字典顺序大于字符串参数则返回一个大于 0 的值)。 所以当单词出现相同的频率按字母顺序排序,需要调用s2.compareTo(s1),因为当s1字典序小于s2时返回值为负(应为正值);
- 对PriorityQueue实现使用的offer及poll方法,都为接口 Queue中的方法,不使用add方法是由于offer方法通常要优于 add(E),后者可能无法插入元素而只是抛出一个异常;
- 时间复杂度:O(nlogk)。其中 n 是 words 的长度,使用O(n) 的时间计算每个单词的频率,然后将 n 个单词添加到堆中,添加每个单词的时间为 O(logk) ;
- 空间复杂度:O(n)
447. Number of Boomerangs 回旋镖的数量
给定平面上 n 对 互不相同 的点 points ,其中 points[i] = [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 ,其中 i 和 j 之间的距离和 i 和 k 之间的距离相等(需要考虑元组的顺序)。返回平面上所有回旋镖的数量。points[i].length == 2。
示例:
输入:points = [[0,0],[1,0],[2,0]]
输出:2
解释:两个回旋镖为 [[1,0],[0,0],[2,0]] 和 [[1,0],[2,0],[0,0]]
思路:
以每个点为枢纽点,遍历n次,以当前枢纽点建立map集合,再遍历n-1次,得到的map集合key为某一其他点到此枢纽点的距离,value为距离枢纽点距离为key的点的个数,对每一次外层循环取map集合的value,总的结果即为当前结果加value * (value - 1)种(eg:当前与枢纽点距离相同为某值的点有5个,从中选两个点作为回旋镖i, j, k的后两个点,共有5 * 4种不同的组合)。
题解:
class Solution {
public int numberOfBoomerangs(int[][] points) {
int result = 0;
for (int i = 0; i < points.length; i++) {
Map<Integer, Integer> disCount = new HashMap<>();
for (int j = 0; j < points.length; j++) {
if (i != j) {
int dis = disQuare(points[i], points[j]);
disCount.put(dis, disCount.getOrDefault(dis, 0) + 1);
}
}
for (int value : disCount.values()) {
result += value * (value - 1); // 当前距离下所有j和k点的不同组合总为value乘以value - 1种
}
}
return result;
}
private int disQuare(int[] a, int[] b) {
return (a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]);
}
}
tips:
- 对于二维数组,数组.length表示的为二维数组的行数;
- 为防止求两点距离时开方产生浮点值,使用距离的平方来衡量两点间的距离是否相等;
- 当前指定距离下与i点距离相同的点只有一个时,value * (value - 1)为0,即对于值为1时此式也可行;
- 定义在循环中的变量一次使用完毕后会被垃圾回收,不需要定义在循环体外面以防重复定义占用空间;
- 使用java.util.Map<K,V>类中的Collection
values() 方法,返回此映射中包含的值的 Collection 视图。 来增强for循环取值; - 时间复杂度:O(n^2);
- 空间复杂度:O(n),定义在循环中的哈希表每一次使用完毕后会被垃圾回收,所以整体只占用了O(n)复杂度的空间。
49. Group Anagrams 字母异位词分组
给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串。所有输入均为小写字母。不考虑答案输出的顺序。
示例:
输入:[“eat”, “tea”, “tan”, “ate”, “nat”, “bat”]
输出:
[
["ate","eat","tea"],
["nat","tan"],
["bat"]
]
思路:
互为字母异位词的两个字符串包含的字母相同,因此两个字符串中的相同字母出现的次数一定是相同的,将每个字母出现的次数使用字符串表示,作为哈希表的键。键的类型为String,内容为从a到z的出现字母拼接此字母的出现次数。
题解:
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> resMap = new HashMap<>();
for (String str : strs) {
int[] freq = new int[26];
for (int i = 0; i < str.length(); i++) {
freq[str.charAt(i) - 'a']++;
}
StringBuffer keySb = new StringBuffer();
for (int i = 0; i < 26; i++) {
if (freq[i] != 0) {
keySb.append((char) (i + 'a')).append(freq[i]);
}
}
String keyStr = keySb.toString();
List<String> value = resMap.getOrDefault(keyStr, new ArrayList<String>());
value.add(str);
resMap.put(keyStr, value);
}
return new ArrayList<List<String>>(resMap.values());
}
}
tips:
- 使用java.lang.StringBuffer类,线程安全的可变字符序列,一个类似于 String 的字符串缓冲区。StringBuffer append(char c) 方法将 char 参数的字符串表示形式追加到此序列,并返回当前对象自身。使用链式编程(如果方法的返回值是一个对象,可以根据对象继续调用方法);
- 通过键获取值时,使用 java.util.Map<K,V>接口类中的default V getOrDefault (Object key, V defaultValue) 方法(JDK1.8 新特性)返回指定键映射到的值,如果此映射不包含该键的映射,则返回 defaultValue。来在第一次获取值时新建值ArrayList
对象; - 返回值使用ArrayList(Collection<? extends E> c) 构造一个包含指定 collection 的元素的列表,这些元素是按照该 collection 的迭代器返回它们的顺序排列的。来构造新的结果集合,且参数使用Map<K,V>类中的Collection
values() 方法(新特性)返回此map集合中包含的值的Collection视图; - 时间复杂度:OO(n*(k+∣Σ∣)),其中 n 是 strs 中的字符串的数量,k 是 strs 中的字符串的的最大长度,Σ 是字符集,在本题中字符集为所有小写字母,∣Σ∣=26;
- 空间复杂度:O(n*(k+∣Σ∣)),需要用哈希表存储全部字符串,而记录每个字符串中每个字母出现次数的数组需要的空间为 O(∣Σ∣),在渐进意义下小于 前者,可以忽略不计。
Ⅴ Hash Table (LUT) 哈希表(查找表)
使用底层实现为哈希表的Set及Map集合等的数组相关题目。查找表(Look-Up Table)是由同一类型的数据元素(或记录)构成的集合。查找操作为根据给定的某个K值,在查找表中寻找一个其键值等于K的数据元素,利用查找表的key及value来解决问题。
219. Contains Duplicate II 存在重复元素 II
给定一个整数数组和一个整数 k,判断数组中是否存在两个不同的索引 i 和 j,使得 nums [i] = nums [j],并且 i 和 j 的差的 绝对值 至多为 k。
示例:
输入:nums = [1,2,3,1], k = 3
输出:true
思路:
查找表+滑动窗口的思路。使用一个Set集合存储滑动窗口(先有一个形成窗口的过程,当窗口的长度为k+1时,窗口的长度不再变化,窗口不断右移直到遇到右边界)中的元素,每次遍历比较新添加进来的元素是否在查找表中已经存在。
题解:
class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
Set<Integer> eles = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
if (eles.contains(nums[i])) return true;
eles.add(nums[i]);
if (eles.size() == k + 1) eles.remove(nums[i - k]);
}
return false;
}
}
tips:
- 时间复杂度:O(n) ;
- 空间复杂度:O(min(n,k)),开辟的额外空间取决于散列表中存储的元素的个数,即滑动窗口的大小 O(min(n,k+1))。
220. Contains Duplicate III 存在重复元素 III
给你一个整数数组 nums 和两个整数 k 和 t 。请你判断是否存在 两个不同下标 i 和 j,使得 abs(nums[i] - nums[j]) <= t ,同时又满足 abs(i - j) <= k 。-2^31 <= nums[i] <= 2^31 - 1。
示例:
输入:nums = [1,0,1,1], k = 1, t = 2
输出:true
题解:
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
TreeSet<Long> eles = new TreeSet<>();
for (int i = 0; i < nums.length; i++) {
Long ceiling = eles.ceiling((long) nums[i] - (long) t);
if (ceiling != null && ceiling <= (long) nums[i] + (long) t) return true;
eles.add((long) nums[i]);
if (eles.size() == k + 1) eles.remove((long) nums[i - k]);
}
return false;
}
}
tips:
- 与219题思路相同,对于序列中每一个元素 x 左侧的至多 k 个元素,如果这 k 个元素中存在一个元素落在区间 [x−t,x+t] 中就找到了一对符合条件的元素;
- 这里不能使用多态来定义TreeSet集合,编译看左边,左边为Set时,Set类当中没有子类TreeSet的ceiling方法,所以编译报错;
- 使用有序集合java.util.TreeSet
类,使用元素的自然顺序对元素进行排序,或者根据创建 set 时提供的 Comparator 进行排序,具体取决于使用的构造方法。 此实现为基本操作(add、remove 和 contains)提供受保证的 log(n) 时间开销; - 使用TreeSet类中的E ceiling(E e) 方法,返回此 set 中大于等于给定元素的最小元素,如果不存在这样的元素,则返回 null。 来判断是否存在一个尽可能小的元素k大于等于当前元素减t,进一步判断其是否满足abs(nums[i] - nums[j]) <= t的要求;
- 时间复杂度:O(n*log(min(n,k))),其中 n 是给定数组的长度。每个元素至多被插入有序集合和从有序集合中删除一次,每次操作时间复杂度均为 O(log(min(n,k));
- 空间复杂度:O(min(n,k)),有序集合中至多包含 min(n,k+1) 个元素。
217. Contains Duplicate 存在重复元素
给定一个整数数组,判断是否存在重复元素。如果存在一值在数组中出现至少两次,函数返回 true 。如果数组中每个元素都不相同,则返回 false 。
示例:
输入:[1,2,3,1]
输出:true
题解:
class Solution {
public boolean containsDuplicate(int[] nums) {
Set<Integer> eles = new HashSet<>();
for (int i = 0; i < nums.length; i++) {
if (!eles.add(nums[i])) return true;
}
return false;
}
}
tips:
- 使用java.util.Set
接口类中的boolean add(E e) 方法,如果 set 中尚未存在指定的元素,则添加此元素。 如果此 set 没有包含满足 (e==null ? e2==null : e.equals(e2)) 的元素 e2,则向该 set 中添加指定的元素 e。如果此 set 已经包含该元素,则该调用不改变此 set 并返回 false。来简化两步contains及add方法的调用; - 时间复杂度:O(n)
- 空间复杂度:O(n)
1. Two Sum 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 的那 两个 整数,并返回它们的数组下标。你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。你可以按任意顺序返回答案。
示例:
输入:nums = [3,2,4], target = 6
输出:[1,2]
思路:
使用Map集合存储数组的值及其索引,对于数组每一个元素 i,首先查询哈希表中是否存在 target - i 再将 i 插入到哈希表中,即能保证同一个元素在答案里不重复出现。
题解:
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> numsMap = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (numsMap.containsKey(complement)) return new int[] {numsMap.get(complement), i};
numsMap.put(nums[i], i);
}
return null;
}
}
tips:
- 时间复杂度:O(n),哈希表插入、查找及删除的时间复杂度均为O(1);
- 空间复杂度:O(n)
454. 4Sum II 四数相加 II
给定四个包含整数的数组列表 A , B , C , D ,计算有多少个元组 (i, j, k, l) ,使得 A[i] + B[j] + C[k] + D[l] = 0。为了使问题简单化,所有的 A, B, C, D 具有相同的长度 N,且 0 ≤ N ≤ 500 。所有整数的范围在 -228 到 228 - 1 之间,最终结果不会超过 2^31 - 1 。
示例:
输入:A = [ 1, 2],B = [-2,-1],C = [-1, 2],D = [ 0, 2]
输出:2
解释:两个元组为 (0, 0, 0, 1) 和 (1, 1, 0, 0)
题解:
class Solution {
public int fourSumCount(int[] nums1, int[] nums2, int[] nums3, int[] nums4) {
int length = nums1.length;
Map<Integer, Integer> combination = new HashMap<>();
int result = 0;
for (int i = 0; i < length; i++) {
for (int j = 0; j < length; j++) {
int key = nums1[i] + nums2[j];
combination.put(key, combination.getOrDefault(key, 0) + 1);
}
}
for (int i = 0; i < length; i++) {
for (int j = 0; j < length; j++) {
int key = nums3[i] + nums4[j];
if (combination.containsKey(-key)) result += combination.get(-key);
}
}
return result;
}
}
tips:
- 与1题思路相同;
- 可以使用-int变量表示一个负数(大小为负的int变量);
- 时间复杂度:O(n^2),哈希表插入、查找及删除的时间复杂度均为O(1);
- 空间复杂度:O(n^2),哈希映射需要使用的空间。在最坏的情况下,A[i]+B[j]的值均不相同,因此值的个数为n^2,也就需要 O(n^2)的空间。
Ⅵ Quick Sort - Partition (Divide and Conquer) 快速排序 - 三路快排(分治算法)
使用快速排序、三路快排的思路。
时间复杂度:O(n) n - 序列长度
空间复杂度:O(1) 没有创建新的序列,只需要常数空间存放若干变量
75. Sort Colors 颜色分类
给定一个包含红色、白色和蓝色,一共 n 个元素的数组,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
示例:
输入:nums = [2,0,1]
输出:[0,1,2]
思路:
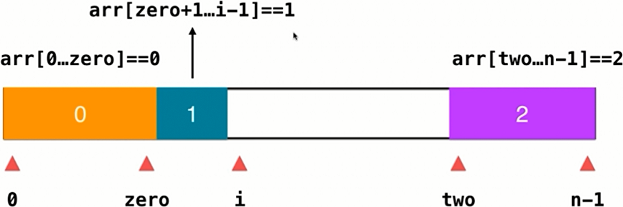
题解:
class Solution {
public void sortColors(int[] nums) {
int zero = -1; // [0, ..., zero]的元素都为0
int two = nums.length; // [two, ..., nums.length - 1]的元素都为2
for (int i = 0; i < two; ) { // 索引i用于遍历
if (nums[i] == 0) {
nums[i++] = nums[++zero];
nums[zero] = 0;
} else if (nums[i] == 2) { // 这里i不能递增,因为和--two处元素交换,--two处的元素为一不确定的值(未检查的值)
nums[i] = nums[--two];
nums[two] = 2;
} else { // nums[i] == 1
i++;
}
}
}
}
215. Kth Largest Element in an Array 数组中的第K个最大元素
在未排序的数组中找到第 k 个最大的元素。
示例:
输入:[3,2,3,1,2,4,5,5,6] 和 k = 4
输出:4
思路:
用快速排序来解决这个问题,先对原数组排序,再返回倒数第 k 个位置,这样平均时间复杂度是 O(nlogn)。每次经过「划分」操作后,一定可以确定一个元素的最终位置,即 x 的最终位置为 q,并且保证 a[l⋯q−1] 中的每个元素小于等于 a[q],且 a[q] 小于等于 a[q+1⋯r] 中的每个元素。所以只要某次划分的 q 为倒数第 k 个下标的时候,就已经找到了答案。 只需关心这一点,至于 a[l⋯q−1] 和 a[q+1⋯r] 是否是有序的,不需要关心。改进快速排序算法:在分解的过程当中,对子数组进行划分,如果划分得到的 q 正好就是需要的下标,就直接返回 a[q];否则,如果 q 比目标下标小,就递归右子区间,否则递归左子区间。这样就可以把原来递归两个区间变成只递归一个区间,提高了时间效率。

题解:
class Solution {
Random random = new Random();
public int findKthLargest(int[] nums, int k) {
int index = nums.length - k; // 第k大元素的索引
return randomPartition(nums, 0, nums.length - 1, index);
}
// 用于判别继续向左半部分还是右半部分划分(迭代),pivot中轴值在下一迭代部分中随机选取
private int randomPartition(int[] nums, int left, int right, int index) {
int pivotIndex = random.nextInt(right - left + 1) + left;
swap(nums, pivotIndex, right); // 将pivot中值交换到数组末尾
int result = partition(nums, left, right);
if (result == index) return nums[result];
return result > index ? randomPartition(nums, left, result - 1, index) : randomPartition(nums, result + 1, right, index);
}
// 划分的方法
private int partition(int[] nums, int left, int right) {
int pivot = nums[right]; // 中轴值(位于数组末尾)
int i = left - 1; // [left, ..., i]的元素都小于pivot,[i + 1, ..., right]的元素都大于等于pivot
for (int j = left; j < right; j++) {
if (nums[j] < pivot) {
swap(nums, ++i, j);
}
}
swap(nums, i + 1, right); // 将中轴值归于正确的位置
return i + 1; // 中轴值的索引
}
// 数组中索引i及索引j处的元素对调位置
private void swap(int[] array, int i, int j) {
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
}
tips:
- 这里也用到了双指针的思想,指针i用于替换元素(慢指针),指针j用于遍历数组(快指针);
- 时间复杂度:O(n),快速排序的性能和「划分」出的子数组的长度密切相关。直观地理解如果每次规模为 n 的问题都划分成 1 和 n - 1,每次递归的时候又向 n−1 的集合中递归,这种情况是最坏的,时间代价是 O(n^2)。这里引入随机化来加速这个过程,它的时间代价的期望是 O(n)。(证明过程:《算法导论》9.2)
- 空间复杂度:O(logn),递归使用栈空间的空间代价的期望为O(logn)。
324. Wiggle Sort II 摆动排序 II
给你一个整数数组 nums,将它重新排列成 nums[0] < nums[1] > nums[2] < nums[3]… 的顺序。你可以假设所有输入数组都可以得到满足题目要求的结果。
示例:
输入:nums = [1,3,2,2,3,1]
输出:[2,3,1,3,1,2]
思路:
将数组从中间位置进行等分(如果数组长度为奇数则将中间的元素分到前子数组),然后将两个子数组进行穿插(第一部分子数组所有元素小于等于第二部分子数组元素)。定义较小的子数组为A,较大的子数组为B,如果nums中存在重复元素,正序穿插可能会造成nums[i] <= nums[i+1] >= nums[i+2] <= nums[i+3]…的情况。由于穿插之后,相邻元素必来自不同子数组,当A或B内部出现重复元素是不会出现上述穿插后相邻元素可能相等的情况。所以上述情况是因为数组A和数组B出现了相同元素,使用r来表示这一元素,如果A和B都存在r,那么r一定是A的最大值,B的最小值,这意味着r一定出现在A的尾部,B的头部。如果这一重复数字的个数较少则不会出现上述情况,只有当这一数字个数达到原数组元素总数的一半,才会在穿插后的出现在相邻位置。要解决这一情况需要使A的r和B的r在穿插后尽可能分开。于是将A和B子数组反序穿插。对于此问题,实际上并不需关心A和B内部的元素顺序,只需要满足A和B长度相同(或相差1),且A中的元素小于等于B中的元素,且r出现在A的头部和B的尾部(反序插入)即可。所以不需要进行排序,而只需要找到数组的中位数,且与中位数相等的值都位于其附近。而寻找中位数可以用快速选择算法(三路快排的思路)实现。

题解:
class Solution {
Random random = new Random();
public void wiggleSort(int[] nums) {
int index = (nums.length - 1) / 2; // 数组中位数的的索引
randomPartition(nums, 0, nums.length -1, index);
int[] nums2 = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
nums2[i] = nums[i];
}
for(int i = index, j = nums.length -1, t = 0; j > index; i--, j--) { // 将较小及较大的子数组进行反序穿插
nums[t++] = nums2[i];
nums[t++] = nums2[j];
}
if (nums.length % 2 == 1) nums[nums.length - 1] = nums2[0]; // 数组的长度为奇数时,将较小子数组的第一个元素补到nums数组末尾
}
// 用于判别继续向左半部分还是右半部分划分(迭代),pivot中轴值在下一迭代部分中随机选取
private void randomPartition(int[] nums, int left, int right, int index) {
int pivotIndex = random.nextInt(right - left + 1) + left;
swap(nums, pivotIndex, right); // 将pivot中值交换到数组末尾
int result = partition(nums, left, right);
if (result == index) return;
if (index < result) {
randomPartition(nums, left, result - 1, index);
} else {
randomPartition(nums, result + 1, right, index);
}
}
// 划分的方法
private int partition(int[] nums, int left, int right) {
int pivot = nums[right]; // 中轴值(位于数组末尾)
int i = left - 1; // [left, ..., i]的元素都小于pivot
int j = right; // [j, ..., right]的元素大于pivot,(i, ..., j)的元素都等于pivot
for (int t = left; t < j;) { // 这里遍历的边界条件判断应为小于j
if (nums[t] < pivot) {
swap(nums, ++i, t++);
} else if (nums[t] > pivot) {
swap(nums, --j, t); // 这里t不能递增,因为和--j处元素交换,--j处的元素为一不确定的值(未检查的值)
} else { // nums[t] == pivot
t++;
}
}
if (j <= right) swap(nums, j++, right); // 将中轴值归于正确的位置,和大于pivot部分的第一个元素交换,故这里j索引就需要后移
return (i + j) / 2; // 中轴值的索引,取(i, ..., j)的中位索引
}
// 数组中索引i及索引j处的元素对调位置
private void swap(int[] array, int i, int j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
tips:
- 这道题结合了75题及215题的思路;
- 将nums1拷贝到nums2时不能使用地址引用的方式,如果nums2指向的是nums的地址,nums2则会随着nums的变化而动态变化。
- 时间复杂度:O(n),快速排序的性能和「划分」出的子数组的长度密切相关。直观地理解如果每次规模为 n 的问题都划分成 1 和 n - 1,每次递归的时候又向 n−1 的集合中递归,这种情况是最坏的,时间代价是 O(n^2)。这里引入随机化来加速这个过程,它的时间代价的期望是 O(n)。(证明过程:《算法导论》9.2)
- 空间复杂度:O(n),需要存储两个子数组,所以空间复杂度为O(n)。
Ⅶ Prefix Sum 前缀和
通常涉及连续子数组的问题,使用前缀和来解决。通过前缀和数组可以轻松得到每个区间(子数组)的和。前缀和数组sum保存数组num前 n 位的和,sum[i] = num[0] + num[1] + … + num[i],则区间(子数组)num[i, …, j]所有元素的和为sum[j] - sum [i - 1]。
560. Subarray Sum Equals K 和为K的子数组
给定一个整数数组和一个整数 k,你需要找到该数组中和为 k 的连续的子数组的个数。
示例:
输入:nums = [1,1,1], k = 2
输出:2 , [1,1] 与 [1,1] 为两种不同的情况。
思路:
定义 pre[i] 为 nums[0..i] 里所有数的和,即以元素i为结尾的前缀和,使用前缀和及哈希表(查找表)的思路,建立哈希表 map,以前缀和为键,出现次数为对应的值,记录 pre[i] 出现的次数。每遍历一个元素i,考虑以 i 结尾的和为 k 的连续子数组个数,只需要统计有多少个前缀和为 pre[i]−k 的 pre[j],即nums[j+1, …, i]连续子数组的和为k,总的数组中和为k的连续子数组的不同种数就为以每遍历的元素i结尾情况的总和。
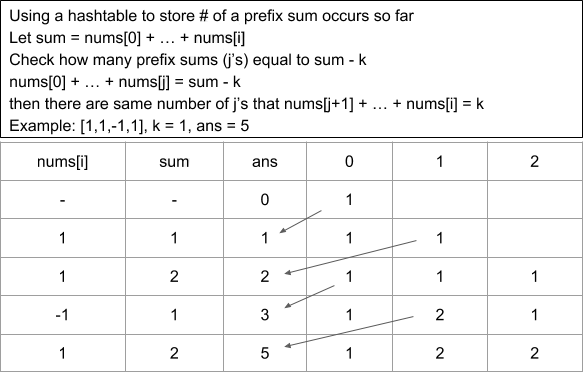
题解:
class Solution {
public int subarraySum(int[] nums, int k) {
Map<Integer, Integer> prefixSumCount = new HashMap<>();
prefixSumCount.put(0, 1); // 前缀和为0的次数为1
int sum = 0;
int result = 0;
for (int i = 0; i < nums.length; i++) {
sum += nums[i];
result += prefixSumCount.getOrDefault(sum - k, 0);
prefixSumCount.put(sum, prefixSumCount.getOrDefault(sum, 0) + 1);
}
return result;
}
}
tips:
- 满足要求的连续子数组可以为当前元素的前缀和(即为nums[0, …, i]),故统计前缀和出现次数的map集合需要初始化为 key 为 0 value 为 1 的键值对;
- 时间复杂度:O(n);
- 空间复杂度:O(n),哈希表在最坏情况下可能有 n 个不同的键值。
523. Continuous Subarray Sum 连续的子数组和
给定一个包含 非负数 的数组和一个目标 整数 k ,编写一个函数来判断该数组是否含有连续的子数组,其大小至少为 2,且总和为 k 的倍数,即总和为 n * k ,其中 n 也是一个整数。
示例:
输入:[23,2,6,4,7], k = 6
输出:true
解释:[23,2,6,4,7]是大小为 5 的子数组,并且和为 42。
思路:
使用前缀和、模运算(同余定理)及哈希表(查找表)的思路,建立哈希表 map,以前缀和对k取模的值为键,当前索引为对应的值。假设第 i 个位置的前缀和的值为 sumRem,如果以 i 为右端点的任何子数组的和是 k 的倍数,假设该子数组左端点位置为 j+1 ,那么哈希表中第 j 个元素保存的值为 (sumRem-n∗k)%k ,其中 n > 0 整数。发现 (sumRem-n∗k)%k=sumRem ,也就是跟第 i 个元素保存到哈希表中的值相同(同理,遍历更新前缀和对k取模的值时,只需每次累加取模后的前缀和)。
令 P[i] = A[0] + A[1] + … + A[i]。那么每个连续子数组的和 sum(i,j) 就可以写成 P[j] - P[i-1](其中 0 < i < j)的形式。此时,判断子数组的和能否被 K 整除就等价于判断 (P[j] - P[i-1]) mod K == 0,根据 同余定理,只要 P[j] mod K == P[i-1] mod K,就可以保证上面的等式成立。
每遍历一个元素i,考虑以 i 结尾的和为 k 的倍数连续子数组是否存在,只需要判断第一个前缀和对k取模的值为当前前缀和对k取模的元素索引 j 与当前元素索引 i 差值是否大于1。与此同时map集合需要初始化,当不截取元素即从第一个元素到当前元素即为满足要求的子数组时,map集合的key为0,value为-1。遍历数组的过程中,为保证满足要求的子数组的长度尽量长,只有找到新的 前缀和%k 的值(即在哈希表中没有这个值),才会往哈希表中插入一条记录 key:sum % k,value:i。
题解:
class Solution {
public boolean checkSubarraySum(int[] nums, int k) {
Map<Integer, Integer> prefixSumRem = new HashMap<>();
prefixSumRem.put(0, -1); // 初始化,前缀和k的余数为0时的索引为-1
int sumRem = 0;
for (int i = 0; i < nums.length; i++) {
sumRem = (sumRem +nums[i]) % k;
if (prefixSumRem.containsKey(sumRem)) {
if (i - prefixSumRem.get(sumRem) > 1) return true;
} else {
prefixSumRem.put(sumRem, i); // 当不包含前缀和k的余数时才加入到map集合
}
}
return false;
}
}
tips:
- 时间复杂度:O(n);
- 空间复杂度:O(min(n, k)),哈希表最多包含 min(n,k) 个不同的元素。
974. Subarray Sums Divisible by K 和可被 K 整除的子数组
给定一个整数数组 A,返回其中元素之和可被 K 整除的(连续、非空)子数组的数目。1 <= A.length <= 30000。
示例:
输入:A = [4,5,0,-2,-3,1], K = 5
输出:7
解释:有 7 个子数组满足其元素之和可被 K = 5 整除,[4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]。
思路:
此题整数数组的元素可能为负数,需要关注模运算背后的机制。通常情况下,在数论中总是使用正余数(即使负数参与了取余运算)。而在计算系统中,a(被除数) 除 n(除数) 得到商 q 和余数 r 满足以下式子:a = n * q + r,q ∈ Z(整数集,…, -2, -1, 0, 1, 2, …),|r| < |n|。在不同的编程语言中,余数的符号取决于编程语言的类型和被除数 a 或除数 n 的符号。对于Java语言,取模运算(余数)结果的符号(正负)与被除数相同;eg:3 % -5 = 3,5 % -3 = 2,-3 % 5 = -3,-5 % 3 = -2;正数对负数取模的运算规则与数论中的运算方法相同,而负数对正数取模的运算规则不同,商 q 与除数 n 的乘积为第一个大于被除数的整数(在数论中商 q 与除数 n 的乘积为第一个小于被除数的整数),由商则可得出模值(余数);有记忆性结论:正数取模负数的结果和正数取模这个负数的绝对值的结果相同,负数取模正数的结果为这个负数的绝对值取模这个正数后加上一个负号。
此题前缀和对K取模可能得到负数,则可以使用将这个负数加上K再次对K取模的方式保证前缀和模值总为正,且此方式来判断连续子数组元素之和是否能被K整除也是正确的。
题解:
class Solution {
public int subarraysDivByK(int[] A, int K) {
Map<Integer, Integer> prefixSumRemCount = new HashMap<>();
prefixSumRemCount.put(0, 1);
int sumRem = 0;
int result = 0;
for (int i = 0; i < A.length; i++) {
sumRem = ((sumRem + A[i]) % K + K) % K;
int value = prefixSumRemCount.getOrDefault(sumRem, 0);
result += value;
prefixSumRemCount.put(sumRem, value + 1);
}
return result;
}
}
tips:
- 结合了560与523题的思路;
- 时间复杂度:O(n);
- 空间复杂度:O(min(n, k))。
930. Binary Subarrays With Sum 和相同的二元子数组
在由若干 0 和 1 组成的数组 A 中,有多少个和为 S 的非空子数组。
示例:
输入:A = [1,0,1,0,1], S = 2
输出:4
解释:[1,0,1,0,1],[1,0,1,0,1],[1,0,1,0,1],[1,0,1,0,1] 为满足题目要求的子数组。
题解:
class Solution {
public int numSubarraysWithSum(int[] A, int S) {
Map<Integer, Integer> prefixSumCount = new HashMap<>();
prefixSumCount.put(0, 1);
int sum = 0;
int result = 0;
for (int i = 0; i < A.length; i++) {
sum += A[i];
result += prefixSumCount.getOrDefault(sum - S, 0);
prefixSumCount.put(sum, prefixSumCount.getOrDefault(sum, 0) + 1);
}
return result;
}
}
tips:
- 与560题思路相同;
- 时间复杂度:O(n);
- 空间复杂度:O(n)
525. Contiguous Array 连续数组
给定一个二进制数组, 找到含有相同数量的 0 和 1 的最长连续子数组(的长度)。
示例:
输入:[0,1,0]
输出:2
解释: [0, 1] (或 [1, 0]) 是具有相同数量0和1的最长连续子数组。
思路:
使用前缀和及哈希表(查找表)的思路,建立哈希表 map,以前缀和为键,当前索引为对应的值。此题关键在于将数组中的所有0变为-1,则含有相同数量的 0 和 1 的连续子数组可以转换为sum of subarray == 0。When the same prefix sum appears at i, j. sum(i+1, …, j) == 0, answer = max(answer, j - i). 遍历数组的过程中,为保证满足要求的子数组的长度尽量长,只有找到新的 前缀和的值(即在哈希表中没有这个值),才会往哈希表中插入一条记录 key:sum,value:i。(Use a hashtable to track the first index of each prefix sum appears)
题解:
class Solution {
public int findMaxLength(int[] nums) {
Map<Integer, Integer> prefixSumIndex = new HashMap<>();
prefixSumIndex.put(0, -1);
int sum = 0;
int maxLen = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] == 0) {
sum += -1; // 将数组中的元素0都转化为-1
} else {
sum += 1;
}
if (prefixSumIndex.containsKey(sum)) {
maxLen = Math.max(maxLen, i - prefixSumIndex.get(sum));
} else {
prefixSumIndex.put(sum, i);
}
}
return maxLen;
}
}
tips:
- 与523题思路相似;
- 时间复杂度:O(n);
- 空间复杂度:O(n),map 最大使用空间为 n ,当且仅当所有元素都是 1 或者 0
Ⅷ Data Structure and Design 数据结构及其设计
使用队列、栈、集合、链表等数据结构的常规题目,以及实现特定功能的数据结构设计题目。
239. Sliding Window Maximum 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。
示例:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置ㅤㅤㅤㅤㅤ最大值
[1 3 -1] -3 5 3 6 7ㅤㅤㅤㅤ3
1 [3 -1 -3] 5 3 6 7ㅤㅤㅤㅤ3
1 3 [-1 -3 5] 3 6 7ㅤㅤㅤㅤ5
1 3 -1 [-3 5 3] 6 7ㅤㅤㅤㅤ5
1 3 -1 -3 [5 3 6] 7ㅤㅤㅤㅤ6
1 3 -1 -3 5 [3 6 7]ㅤㅤㅤㅤ7
思路:
有序双端队列(有序的也即为单调队列)的思路。遍历数组,使用一个队列存储所有还没有被移除的下标(并非值)。在队列中,这些下标按照从小到大的顺序被存储,并且它们在数组 nums 中对应的值是严格单调递减的。当滑动窗口向右移动时,需要把一个新的元素放入队列中。如果当前遍历的数(窗口移动时的新增元素)比队尾的值大,则需要不断弹出队尾值,直到队列重新满足从大到小的要求,再添加当前遍历的数(因为之前比当前遍历的数小的元素的值之后滑动窗口选取元素最大值的时候一定用不上)。刚开始遍历时,有一个形成窗口的过程,当窗口大小形成(遍历到第一个窗口的最后一个索引)后,每次移动时,判断队首的值的数组下标是否在滑动窗口中,如果在则需要弹出队首的值,当前窗口的最大值即为队首的数。

题解:
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int[] result = new int[nums.length - k + 1];
Deque<Integer> deque = new LinkedList<Integer>(); // 双端队列
for (int i = 0; i < nums.length; i++) {
while (deque.size() > 0 && nums[i] > nums[deque.getLast()]) deque.removeLast();
deque.addLast(i); // 如果当前遍历的数比队尾的值大,则需要不断弹出队尾值,直到队列重新满足从大到小的要求,再添加当前遍历的数
if (i - k + 1 >= 0) result[i - k + 1] = nums[deque.getFirst()]; // 当前窗口的最大值即为队首的数
if (i - k + 1 >= deque.getFirst()) deque.removeFirst(); // 判断队首的值的数组下标是否在滑动窗口中,如果在则需要弹出队首的值
}
return result;
}
}
tips:
- 对java.util.Queue< E > 接口类的熟悉;
- 时间复杂度:O(n);
- 空间复杂度:O(k),新增最大长度为k的双端队列。
150. Evaluate Reverse Polish Notation 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。整数除法只保留整数部分。给定逆波兰表达式总是有效的。
示例:
输入:tokens = [“4”,”13”,”5”,”/”,”+”]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
思路:
使用栈结构辅助计算。逆波兰表达式即后缀表达式,运算符位于操作数之后。逆波兰表达式的计算求值:从左至右扫描表达式,遇到数字时将数字压入堆栈,遇到运算符时弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈,重复上述过程直到表达式最右端,最后运算得出的值(栈中最后的一个元素)即为表达式的结果。
题解:
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> numStack = new Stack<>();
for (String str : tokens) {
if (str.length() == 1 && (str.charAt(0) < '0' || str.charAt(0) > '9')) { // 为运算符:弹出栈顶元素两次进行运算
int ele1 = numStack.pop(); // 一次运算的主动数(后者参与运算的数,eg:8-2的2 或 6/3的3)
int ele2 = numStack.pop(); // 一次运算的被动数(前者参与运算的数,eg:8-2的8 或 6/3的6)
switch (str.charAt(0)) {
case '+':
numStack.push(ele2 + ele1);
break;
case '-':
numStack.push(ele2 - ele1);
break;
case '*':
numStack.push(ele2 * ele1);
break;
default: // 运算符为除号
numStack.push(ele2 / ele1);
break;
}
} else numStack.push(Integer.parseInt(str)); // 为一数字:直接入栈
}
return numStack.pop();
}
}
tips:
对于 switch 语句:
- 多个case后面的数值不可以重复;
- switch后面的小括号当中只能是下列数据类型:基本数据类型:byte/short/char/int,引用数据类型:String字符串/enum枚举;
- switch语句格式可以很灵活:前后顺序可以颠倒,而且break语句还可以省略(匹配哪一个case就从哪一个位置向下执行,直到遇到了break或者整体结束为止:当程序判断某个case的条件为真后,它将在执行该case所带的的语句块(此语句块无 break 语句)之后,不再对后面的case的条件进行判断而直接执行);
- 时间复杂度:O(n)
- 空间复杂度:O(n),栈中元素的个数不会超过逆波兰表达式的长度n
224. Basic Calculator 基本计算器
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。s 由数字、’+’、’-‘、’(‘、’)’、和 ‘ ‘ 组成。
示例:
输入:”+48 + -48”ㅤ |ㅤ “(1)” ㅤ|ㅤ “-(-1 - -1)”ㅤ | ㅤ”(1+(4+5+2)-3)+(6+8)”
输出:ㅤㅤ 0ㅤ ㅤㅤ |ㅤ ㅤ 1 ㅤ | ㅤ ㅤ2ㅤㅤ ㅤ | ㅤㅤㅤㅤㅤ23
思路:
利用辅助栈解决括号问题。将一个表达式分为左边的表达式、运算符和右边的表达式三部分,左边或者右边的表达式可以是一个数字也可以是一个对括号包起来的表达式,运算符可以是加减。对于一个只包含加减和括号的表达式,可以从左到右计算,遇到括号就先计算括号里的,即先计算左边的表达式,然后将左边表达式的结果和运算符保存起来,再计算右边表达式,最后计算总的结果:左边表达式的结果由中间运算符和右边表达式的结果的结果。
这里表达式的结果是:有一个数字(右边的表达式计算的结果)取其前面的符号(中间的运算符)累加到已有结果(左边的表达式计算的结果)中(使用加号为 1 减号为 -1 乘以当前数字);或者有一个右括号取出栈中的符号即与此右括号匹配的左括号的左边的符号(中间的运算符),并将当前数字更新为此括号内计算出来的结果(右边的表达式计算的结果),取出栈中的数字即此括号前的计算结果(左边的表达式计算的结果)。
当表达式出现括号则用栈保存括号前的左边的表达式计算的结果和中间的运算符,符号与左边表达式的结果都置为默认值以计算右边表达式的结果(出现括号但是符号变量和结果变量都需要置默认,只能将之前的符号和结果存储与栈中)。
对于多层嵌套括号的情况:栈顶保留的是最里层嵌套的运算,弹出栈的时候,正好先算的是最里面括号的,再算外边括号的。eg:对于 (1 + (2 + (3 + 4))),栈里面保存的是 [“1”, “+”, “2”, “+”],然后遇到 3,此时计算的是 0 + 3,然后算 3 + 4,再算 2 + 7,再算 1 + 9。
题解:
class Solution {
public int calculate(String s) {
int res = 0; // 左边表达式除去栈内保存元素的计算结果(括号外的部分计算结果或者括号内的计算结果),默认值为0
int num = 0; // 当前遇到的数字(右边表达式的结果),会产生运算并将结果更新到 res 中
int sign = 1; // 中间的运算符:加号为1减号为-1,默认值为1
Stack<Integer> stack = new Stack<>(); // 用于存储括号外的结果
char[] chs = s.toCharArray();
for (int i = 0; i < chs.length; i++) {
if (chs[i] == ' ') continue; // 跳过空格
if (chs[i] >= '0' && chs[i] <= '9') {
num = num * 10 + chs[i] - '0'; // 多位数则需要累加
if (i + 1 < chs.length && chs[i + 1] >= '0' && chs[i + 1] <= '9') continue; // 数字可能不止一位数,当下一字符不为数字则产生运算
} else if (chs[i] == '+' || chs[i] == '-') {
num = 0; // 需要将 num 置0,以存放当前符号之后的数字(同时遍历到符号不应产生运算)
sign = chs[i] == '+' ? 1 : -1;
} else if (chs[i] == '(') {
stack.push(res); // 将左括号之前的临时结果入栈(即左边表达式的计算结果)
stack.push(sign); // 将左括号左边的运算符入栈(即中间的运算符)
res = 0; // 将 res 置0,以保存括号中的计算结果(即右边表达式的计算结果)
sign = 1; // 将符号置为默认值
} else { // 当前字符为右括号')'
sign = stack.pop(); // 将此右括号对应的左括号左边的运算符弹出(即中间的运算符)
num = res; // 将num更新为括号中的计算结果(即右边表达式的计算结果):更新num值应在更新res值之前,因为num值引用了:原来res的值
res = stack.pop(); // 更新res的值(此右括号对应的左括号左边的左边表达式的计算结果):新的res的值
}
res += sign * num; // 运算
}
return res;
}
}
tips:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
227. Basic Calculator II 基本计算器 II
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。整数除法仅保留整数部分。s 由整数和算符 (‘+’, ‘-‘, ‘*’, ‘/’) 组成,中间由一些空格隔开。表达式中的所有整数都是非负整数,且在范围 [0, 2^31 - 1] 内。
示例:
输入:s = “ 3+5 / 2 “
输出:5
思路:
使用辅助栈存储加减运算的结果(乘除运算则先取出栈顶元素计算完再入栈)。由于乘除优先于加减计算,先进行所有乘除运算,并将这些乘除运算后的整数值放回原表达式的相应位置,则随后整个表达式的值就等于一系列整数加减后的值。使用一个栈保存 进行乘除运算后的 整数的值。
使用一个变量 preSign 记录每个数字之前的运算符,每次遍历到数字末尾时由 preSign 决定计算方式:加号则数字压入栈,减号则将数字取反压入栈,乘除号则计算数字与栈顶元素(先弹出)的结果压入栈。
遍历完字符串表达式 s 后,将栈中元素累加即为该字符串表达式的值。
题解:
class Solution {
public int calculate(String s) {
Stack<Integer> stack = new Stack<>(); // 存储加减运算的结果(乘除运算则先取出栈顶元素计算完再入栈)
char preSign = '+'; // 产生运算时的前一个运算符(数字前面的运算符),默认值为 '+'
int num = 0; // 当前数字
char[] chs = s.toCharArray();
for (int i = 0; i < chs.length; i++) {
if (Character.isDigit(chs[i])) num = num * 10 + chs[i] - '0'; // 为一数字则继续累加到当前数字
if (!Character.isDigit(chs[i]) && chs[i] != ' ' || i == chs.length - 1) { // 为一运算符(不为空格也不为数字)或者遍历到字符串表达式的末尾:表示当前数字累加完需要进行运算入栈或者直接入栈
switch (preSign) { // 这里判断的符号因为产生运算时的前一个运算符(数字前面的运算符)而不是当前的运算符
case '+':
stack.push(num);
break;
case '-':
stack.push(-num);
break;
case '*':
stack.push(stack.pop() * num);
break;
default: // 运算符为除号
stack.push(stack.pop() / num);
break;
}
preSign = chs[i]; // 更新 preSign 的值:即为下一次运算的运算符
num = 0; // 当前数字计算完之后需要置0(因为 num 是累加求值)
} // 空格则不满足上述两个 if 判断而跳过
}
int result = 0;
while (!stack.empty()) result += stack.pop();
return result;
}
}
tips:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
71. Simplify Path 简化路径
给你一个字符串 path ,表示指向某一文件或目录的 Unix 风格 绝对路径 (以 ‘/’ 开头),请你将其转化为更加简洁的规范路径。在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外,两个点 (..) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠(即,’//’)都被视为单个斜杠 ‘/’ 。 对于此问题,任何其他格式的点(例如,’…‘)均被视为文件/目录名称。返回的 规范路径 必须遵循下述格式:始终以斜杠 ‘/’ 开头;两个目录名之间必须只有一个斜杠 ‘/’ ;最后一个目录名(如果存在)不能 以 ‘/’ 结尾;此外,路径仅包含从根目录到目标文件或目录的路径上的目录(即,不含 ‘.’ 或 ‘..’)。返回简化后得到的 规范路径 。path 由英文字母,数字,’.’,’/’ 或 ‘_’ 组成。path 是一个有效的 Unix 风格绝对路径。
示例:
输入:path = “/a/./b/../../c/”
输出:”/c”
思路:
使用双端队列存储路径的简化目录结构。由 ”/“ 拆分原路径字符串得到每级目录的名称,遍历目录名称数组,当目录名称为 “.” (表示为当前目录)或 “” (表示原两级目录之间使用了 // 来分隔)时则跳过,为 “..” (表示返回上级目录)则删除双端队列的末尾元素,为其他字符串则表示其为一个有效的目录名称,将其添加到双端队列的末尾。按顺序弹出双端队列的首元素并拼接目录层级分隔符 ”/“添加到结果中,即为简化后的路径。
题解:
class Solution {
public String simplifyPath(String path) {
Deque<String> deque = new LinkedList<>();
String[] dirs = path.split("/");
for (int i = 0; i < dirs.length; i++) {
if (dirs[i].equals(".") || dirs[i].equals("")) continue;
if (dirs[i].equals("..")) {
deque.pollLast(); // 无需判断双端队列是否为空,pollLast() 方法在双端队列为空时返回 null
} else deque.offer(dirs[i]);
}
StringBuilder result = new StringBuilder();
while (!deque.isEmpty()) result.append("/").append(deque.pollFirst());
return result.toString().equals("") ? "/" : result.toString(); // 可能结果为根目录但是字符串为空则需要以 '/' 表示
}
}
tips:
- 对于 java.lang.String 类中的 String[] split(String regex) 方法,根据给定正则表达式的匹配拆分此字符串。eg:”h//a/f///d”.split(“/”) 会将字符串拆分为 [“h”, “”, “a”, “f”, “”, “”, “d”],会出现空字符串;
- 时间复杂度:O(n)
- 空间复杂度:O(n)
Ⅸ Union Find 并查集
并查集一般用于解决深度优先搜索(回溯)问题。
547. Number of Provinces 省份数量
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。返回矩阵中 省份 的数量。1 <= n <= 200,n == isConnected.length,n == isConnected[i].length,isConnected[i][j] 为 1 或 0,isConnected[i][i] == 1,isConnected[i][j] == isConnected[j][i]。
示例:
输入:isConnected = [[1,1,0],[1,1,0],[0,0,1]]
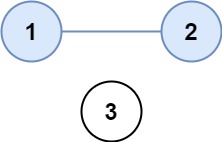
输出:2
思路:
并查集是一种树型的数据结构,用于处理一些不相交集合(disjoint sets)的合并及查询问题。并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。并查集的典型应用是有关连通分量的问题。并查集解决单个问题(添加,合并,查找)的时间复杂度都是O(1)。
数据结构:并查集跟树有些类似,只不过它跟树是相反的。在树这个数据结构里面,每个节点会记录它的子节点。在并查集里,每个节点会记录它的父节点。如果节点是相互连通的(从一个节点可以到达另一个节点),那么他们在同一棵树里,或者说在同一个集合里,或者说他们的祖先是相同的。
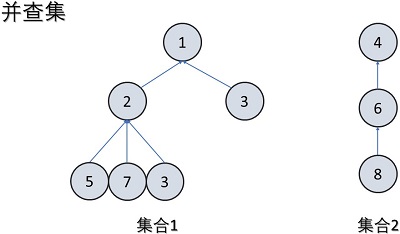
初始化:把每个点所在集合初始化为其自身,即把一个新节点添加到并查集中,它的父节点应该为空。
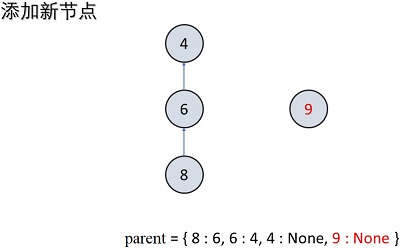
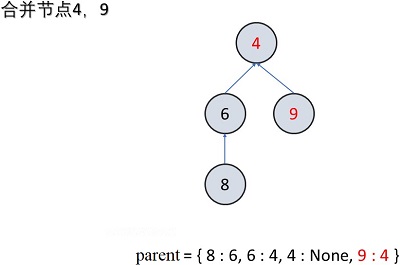
合并:将两个元素所在的集合合并为一个集合。如果两个节点是连通的,那么就需要将它们合并,也就是它们的祖先是相同的。这里将谁当做父节点一般没有区别。
两节点是否连通:判断两个节点是否处于同一个连通分量的,即判断它们的祖先是否相同。
查找:查找元素所在的集合,即根节点。
优化路径压缩:每次查找的时候,如果路径较长(树很深),则修改信息,将树的深度固定为二,以便下次查找的时候速度更快。
对于此题,即为求解连通分量(集合)的数目,需要在模板中额外添加一个变量去跟踪集合的数量(有多少棵树),在初始化的时候将集合数量加一,合并的时候将集合数量减一。
题解:
class Solution {
public int findCircleNum(int[][] isConnected) {
UnionFind unionFind = new UnionFind();
for (int i = 0; i < isConnected.length; i++) {
unionFind.add(i); // 在判断两节点是否相连之前,此两节点都已加入到并查集中
for (int j = 0; j < i; j++) { // 邻接矩阵为关于对角线对称,只需访问对角线外的一半三角形区域即可
if (isConnected[i][j] == 1) unionFind.merge(i, j);
}
}
return unionFind.getTreeNum();
}
}
class UnionFind { // 并查集类
private Map<Integer, Integer> parent; // 存储 key 的父节点 value 的散列表
private int treeNum; // 统计不同根节点的数量(即树的数量)
public UnionFind() { // 并查集初始化
this.parent = new HashMap<>();
this.treeNum = 0;
}
public void add(int x) { // 节点初始化
if (!parent.containsKey(x)) { // 当并查集中不存在此节点,初始化(添加)节点
parent.put(x, null); // 其暂时没有父节点
treeNum++; // 相当于一颗独立的树(一个不相交的独立集合)
}
}
public void merge(int x, int y) { // 合并(连接)两个节点
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) { // 父节点不相同,则表示此两节点不相连,需要合并
parent.put(find(x), find(y)); // 将两节点的父节点连接即可
treeNum--; // 独立子树的数量减一
}
}
public int find(int x) { // 查找节点的父节点
int root = x; // 保存节点的父节点
while (parent.get(root) != null) { // 迭代查找父节点(当前节点所在树的根节点)
root = parent.get(root);
}
while (x != root) { // 迭代将当前节点所在路径的全部节点都直接连接到父节点
int directRoot = parent.get(x);
parent.put(x, root);
x = directRoot;
}
return root;
}
public boolean isConnected(int x, int y) { // 判断两节点是否相连(间接/直接相连)
return find(x) == find(y);
}
public int getTreeNum() { // 获取私有成员变量 treeNum
return this.treeNum;
}
}
tips:
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
Ⅹ Greedy Algorithm 贪心算法
贪心算法,指在对问题进行求解时,在每一步选择中都采取最好或者最优(即最有利)的选择,从而能够导致结果是最好或者最优的算法。
贪婪算法所得到的结果不一定是最优的结果(有时候会是最优解),但是都是相对近似(接近)最优解的结果。
使用到每一步选择都采取最优或最差的情况(贪心)的思想,也为贪心算法。
678. Valid Parenthesis String 有效的括号字符串
给定一个只包含三种字符的字符串:( ,) 和 *,写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则:任何左括号 ( 必须有相应的右括号 );任何右括号 ) 必须有相应的左括号 ( ;左括号 ( 必须在对应的右括号之前 ); *可以被视为单个右括号 ) ,或单个左括号 ( ,或一个空字符串;一个空字符串也被视为有效字符串。字符串大小将在 [1,100] 范围内。
示例:
输入:”(*))”
输出:true
思路:
贪心算法。定义变量 low 及 high 表示字符串括号匹配过程中未配对左括号数量的上下界,遍历字符串,当遇到左括号则 low++,high++;遇到星号则 low–,high++(星号可以被视为单个右括号或左括号);遇到右括号则 low–,high–。
在更新 low 的过程中其不能小于 0(当 low 小于 0 时则将其更新为 0):未配对的左括号数量一定大于等于0,eg:()**( 的情况,未配对的左括号不能为-1或-2个(low),但是可以为1或2个(high)。
当 high 小于 0 直接返回 false:表示将星号全部看作左括号也不够和存在的右括号进行匹配。
字符串遍历完毕当 low 不等 0 则返回 false:代表有多余的左括号未匹配完毕。
题解:
class Solution {
public boolean checkValidString(String s) {
int low = 0, high = 0;
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
low += ch == '(' ? 1 : -1;
high += ch == ')' ? -1 : 1;
if (high < 0) return false; // 满足需要继续判断,不满足则直接返回(结束方法)的思想
if (low < 0) low = 0;
}
return low == 0;
}
}
tips:
- 时间复杂度:O(N),iterate through the string once
- 空间复杂度:O(1)
45. Jump Game II 跳跃游戏 II
给你一个非负整数数组 nums ,你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。你的目标是使用最少的跳跃次数到达数组的最后一个位置。假设你总是可以到达数组的最后一个位置。1 <= nums.length <= 10^4。0 <= nums[i] <= 1000。
示例:
输入:nums = [2,3,1,1,4]
输出:2
解释:跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
思路:
记忆化BFS:一个位置可能多次访问。
贪心:维护上一次跳跃可以到达的最远距离及当前可以到达的最远距离。
题解:
// 贪心
class Solution {
public int jump(int[] nums) {
int end = 0; // 上一次跳跃可以到达的右边界(最远位置)
int max = 0; // 当前最远可以到达的位置
int result = 0; // 当前跳跃次数+1
for (int i = 0; i < nums.length - 1; i++) { // 最后一个位置不需要访问,跳跃次数之前就已经+1(如果end=最后一个位置时,会导致结果多一步)
max = Math.max(max, i + nums[i]);
if (i == end) { // 当前位置为上一次跳跃可以到达的最远位置,需要将步数加一
end = max; // 下一次跳跃可以到达的右边界为前一次跳跃可以到达位置中能跳跃的最远位置
result++;
}
}
return result;
}
}
// 记忆化BFS:一个位置可能多次访问
/*class Solution {
public int jump(int[] nums) {
Queue<Integer> queue = new LinkedList<>();
boolean[] isVisited = new boolean[nums.length];
queue.add(0);
isVisited[0] = true;
int result = 0;
while (!queue.isEmpty()) {
int count = queue.size();
while (count != 0) {
int cur = queue.poll();
if (cur == nums.length - 1) return result;
for (int i = 1; i <= nums[cur]; i++) {
if (cur + i >= nums.length || isVisited[cur + i]) continue;
queue.offer(cur + i);
isVisited[cur + i] = true;
}
count--;
}
result++;
}
return -1;
}
}*/
tips:
- 时间复杂度:O(n)
- 空间复杂度:O(1)
Ⅺ Depth First Search 深度优先搜索
使用深度优先搜索的数组题目。
1306. Jump Game III 跳跃游戏 III
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。请你判断自己是否能够跳到对应元素值为 0 的 任一 下标处。注意,不管是什么情况下,你都无法跳到数组之外。0 <= arr[i] < arr.length。
示例:
输入:arr = [4,2,3,0,3,1,2], start = 5
输出:true
解释:到达值为 0 的下标 3 有以下可能方案:下标 5 -> 下标 4 -> 下标 1 -> 下标 3;下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
思路:
深度优先搜索,将访问过的位置置为-1(标记)。
题解:
class Solution {
public boolean canReach(int[] arr, int start) { // 深度优先搜索
if (start < 0 || start >= arr.length || arr[start] == -1) return false;
int step = arr[start];
arr[start] = -1; // 代表已访问过当前位置
return step == 0 || canReach(arr, start + step) || canReach(arr, start - step); // 由短路特性,到达0则不断回溯,只有当无法到达(可以到达的位置都置为-1)返回false
}
}
tips:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
Ⅻ General - Array & Math 常规 - 数组和数学
常规数组题目,遍历,条件判断,… 。以及数学题。
时间复杂度:O(n) n - 序列长度
空间复杂度:O(1) 没有创建新的序列,只需要常数空间存放若干变量
414. Third Maximum Number 第三大的数
给你一个非空数组,返回此数组中 第三大的数 。如果不存在,则返回数组中最大的数。
示例:
输入:[2, 2, 3, 1]
输出:1
思路:
条件判断的顺序,跳出循环。
题解:
class Solution {
public int thirdMax(int[] nums) {
long m1 = Long.MIN_VALUE; // 第一大的数
long m2 = Long.MIN_VALUE; // 第二大的数
long m3 = Long.MIN_VALUE; // 第三大的数
for (int i = 0; i < nums.length; i++) {
if (nums[i] == m1 || nums[i] == m2 || nums[i] == m3) continue; // 每次循环开始不能少了这句判断,continue表示结束本次循环,继续下一次的循环
if (nums[i] > m1) {
m3 = m2;
m2 = m1;
m1 = nums[i];
} else if (nums[i] > m2) {
m3 = m2;
m2 = nums[i];
} else if (nums[i] > m3) {
m3 = nums[i];
}
}
return m3 == Long.MIN_VALUE ? (int) m1 : (int) m3; // 这里使用强制类型转换,nums[i]的范围为int类型的范围,故不会溢出报错
}
}
tips:
- 不能使用快速排序算法的思路,要求返回的是数组中第三大的数,不是第三大的元素;
- 题目要求-2^31 <= nums[i] <= 2^31 - 1(int类型的取值范围),故第一二三大的数初始值应取long类型的最小取值;
- 当数据类型不一样时,将会发生数据类型转换,此题比较运算及赋值运算发生了自动类型转换;
- 为防止第一二三大的数中出现重复值,每次循环的开始都需要先判断nums[i]是否等于这三个数中的任意一个。
135. Candy 分发糖果
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。你需要按照以下要求,帮助老师给这些孩子分发糖果:每个孩子至少分配到 1 个糖果;评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果。那么这样下来,老师至少需要准备多少颗糖果。
示例:
输入:[1,0,2]ㅤ|ㅤ[1,2,2]
输出:5ㅤ|ㅤ4
解释:给这三个孩子分发 2、1、2 颗糖果ㅤ|ㅤ给这三个孩子分发 1、2、1 颗糖果
思路:
模拟。A与B相邻,先从左至右遍历,当A<B时,使B的糖果数比A多一,使用数组left记录;再从右至左遍历,当A>B时,使A的糖果数比B多一,使用数组right记录。
结果:取left数组与right数组中的最大值即结果。
原因:对于A>B时,先从左至右遍历后,A的糖果数一定大于等于B,且等于情况也只能是A和B糖果数都为1;再从右至左遍历后,A的糖果数一定大于等于B;则取最大值满足要求。
题解:
class Solution {
public int candy(int[] ratings) {
int[] left = new int[ratings.length];
int[] right = new int[ratings.length];
Arrays.fill(left, 1); // 先都分发1颗糖
Arrays.fill(right, 1); // 先都分发1颗糖
for (int i = 1; i < ratings.length; i++) {
if (ratings[i] > ratings[i - 1]) left[i] = left[i - 1] + 1;
}
int result = left[ratings.length - 1];
for (int i = ratings.length - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1]) right[i] = right[i + 1] + 1;
result += Math.max(left[i], right[i]);
}
return result;
}
}
tips:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
165. Compare Version Numbers 比较版本号
给你两个版本号 version1 和 version2 ,请你比较它们。版本号由一个或多个修订号组成,各修订号由一个 ‘.’ 连接。每个修订号由 多位数字 组成,可能包含 前导零 。每个版本号至少包含一个字符。修订号从左到右编号,下标从 0 开始,最左边的修订号下标为 0 ,下一个修订号下标为 1 ,以此类推。例如,2.5.33 和 0.1 都是有效的版本号。比较版本号时,请按从左到右的顺序依次比较它们的修订号。比较修订号时,只需比较 忽略任何前导零后的整数值 。也就是说,修订号 1 和修订号 001 相等 。如果版本号没有指定某个下标处的修订号,则该修订号视为 0 。例如,版本 1.0 小于版本 1.1 ,因为它们下标为 0 的修订号相同,而下标为 1 的修订号分别为 0 和 1 ,0 < 1 。返回规则如下:如果 version1 > version2 返回 1,如果 version1 < version2 返回 -1,除此之外返回 0。1 <= version1.length, version2.length <= 500。version1 和 version2 都是 有效版本号,version1 和 version2 的所有修订号都可以存储在 32 位整数 中。
示例:
输入:version1 = “1.01”, version2 = “1.001.0”
输出:0
解释:忽略前导零,”01” 和 “001” 都表示相同的整数 “1”; 没有指定下标为 2 的修订号,即视为 “0”
思路:
定义 index1 及 index2 为遍历版本号字符串 version1 及 version2 的索引,外层 for 循环用于判断每个修订号数字的大小(每执行一次循环体索引 +1 为跳过小数点:内层 while 循环访问到小数点结束),内层两个 while 循环用于获取相同下标的修订号数字,num1 及 num2(相同下标的修订号数字)需要在每次比较相同下标的修订号大小前重新置于 0:用于忽略前导零,且当一个修订号的下标长度小于另一修订号的下标长度时可以将较小修订号下标长度的修订号“空位”看作 0。
题解:
class Solution {
public int compareVersion(String version1, String version2) {
for (int index1 = 0, index2 = 0; index1 < version1.length() || index2 < version2.length(); index1++, index2++) {
int num1 = 0, num2 = 0;
while (index1 < version1.length() && version1.charAt(index1) != '.') num1 = num1 * 10 + version1.charAt(index1++) - '0';
while (index2 < version2.length() && version2.charAt(index2) != '.') num2 = num2 * 10 + version2.charAt(index2++) - '0';
if (num1 < num2) return -1;
if (num1 > num2) return 1;
}
return 0;
}
}
tips:
- 时间复杂度:O(max(m, n)),m为version1的长度,n为version2的长度
- 空间复杂度:O(1)
1002. Find Common Characters 查找常用字符
给定仅有小写字母组成的字符串数组 A,返回列表中的每个字符串中都显示的全部字符(包括重复字符)组成的列表。例如,如果一个字符在每个字符串中出现 3 次,但不是 4 次,则需要在最终答案中包含该字符 3 次。你可以按任意顺序返回答案。A中只包括小写字母。
示例:
输入:[“bella”,”label”,”roller”]
输出:[“e”,”l”,”l”]
思路:
使用频度数组记录每个字符串中字母出现的次数,每次遍历完一个字符串的所有元素将此字符串的频度数组与结果数组进行比较取最小值。
题解:
class Solution {
public List<String> commonChars(String[] A) {
int[] resArray = new int[26];
Arrays.fill(resArray, Integer.MAX_VALUE);
for (String str : A) {
int[] freq = new int[26];
for (int i = 0; i < str.length(); i++) {
freq[str.charAt(i) - 'a']++;
}
for (int i = 0; i < 26; i++) {
resArray[i] = Math.min(resArray[i], freq[i]);
}
}
List<String> resList = new ArrayList<>();
for (int i = 0; i < 26; i++) {
for (int j = 0; j < resArray[i]; j++) {
resList.add(String.valueOf((char) (i + 'a')));
}
}
return resList;
}
}
tips:
- 结果list集合添加元素使用java.lang.String类中的static String valueOf(char c) 方法,返回 char 参数的字符串表示形式;
- 时间复杂度:(n*(m+∣Σ∣)),其中 n 是数组 A 的长度(即字符串的数目),m 是字符串的平均长度,Σ 为字符集,此题中字符集为所有小写字母,∣Σ∣=26。由于最终答案包含的字符个数不会超过最短的字符串长度,因此构造最终答案的时间复杂度为 O(m+∣Σ∣)。这一项在渐进意义上小于前者,可以忽略;
- 空间复杂度:O(∣Σ∣),除计算存储答案之外的空间。
242. Valid Anagram 有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。你可以假设字符串只包含小写字母。
示例:
输入:s = “anagram”, t = “nagaram”
输出:true
题解:
class Solution {
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) return false;
int[] sFreq = new int[26];
int[] tFreq = new int[26];
for (int i = 0; i < s.length(); i++) { // 字符串s与t长度相同
sFreq[s.charAt(i) - 'a']++;
tFreq[t.charAt(i) - 'a']++;
}
if (Arrays.equals(sFreq, tFreq)) {
return true;
} else {
return false;
}
}
}
tips:
- 时间复杂度:O(n)
- 空间复杂度:O(∣Σ∣),其中 Σ 表示字符集(即字符串中可以出现的字符),∣Σ∣ 表示字符集的大小。此题字符集(所有大写字母 )为所有 ASCII 码在 [65, 90] 内的字符,即∣Σ∣=26
415. Add Strings 字符串相加
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和。num1 和num2 的长度都小于 5100,num1 和num2 都只包含数字 0-9,num1 和num2 都不包含任何前导零,你不能使用任何內建 BigInteger 库, 也不能直接将输入的字符串转换为整数形式。
示例:
输入:num1 = “99”, num2 = “999”
输出:”1098”
题解:
class Solution {
public String addStrings(String num1, String num2) {
boolean flag = false; // 用于标记当前位是否需要进位
StringBuilder result = new StringBuilder();
for (int i = num1.length() - 1, j = num2.length() - 1; i >= 0 || j >= 0; i--, j--) {
int ele1 = i < 0 ? 0 : num1.charAt(i) - '0';
int ele2 = j < 0 ? 0 : num2.charAt(j) - '0';
int sum = flag ? ele1 + ele2 + 1 : ele1 + ele2;
flag = sum >= 10 ? true : false;
result.append(sum % 10);
}
if (flag) result.append(1); // 原字符串最高位还需要进位则结果字符串还需拼接1
return result.reverse().toString();
}
}
tips:
- 整型直接相加会产生溢出错误。使用模拟的思路,模拟两个数手动相加的过程;
- java.lang.StringBuilder 类中的 append() 方法(始终将这些字符添加到生成器的末端)比 insert() 方法(在指定的位置添加字符)效率高,故使用 append() 方法添加每位的计算结果再 调用 StringBuilder reverse() 方法,将此字符序列用其反转形式取代;
- 时间复杂度:O(max(len1, len2))
- 空间复杂度:O(1)
67. Add Binary 二进制求和
给你两个二进制字符串,返回它们的和(用二进制表示)。输入为 非空 字符串且只包含数字 1 和 0。每个字符串仅由字符 ‘0’ 或 ‘1’ 组成。1 <= a.length, b.length <= 10^4。字符串如果不是 “0” ,就都不含前导零。
示例:
输入:a = “1010”, b = “1011”
输出:”10101”
题解:
class Solution {
public String addBinary(String a, String b) {
boolean flag = false;
StringBuilder result = new StringBuilder();
for (int i = a.length() - 1, j = b.length() - 1; i >=0 || j >= 0 || flag; i--, j--) {
int bit1 = i < 0 ? 0 : a.charAt(i) - '0';
int bit2 = j < 0 ? 0 : b.charAt(j) - '0';
int sum = flag ? bit1 + bit2 + 1 : bit1 + bit2;
flag = sum >= 2 ? true : false;
result.append(sum % 2);
}
return result.reverse().toString();
}
}
tips:
- 思路与415题相同。整型直接相加会产生溢出错误;
- 时间复杂度:O(max(len1, len2))
- 空间复杂度:O(1)
43. Multiply Strings 字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。num1 和 num2 的长度小于110。num1 和 num2 只包含数字 0-9。num1 和 num2 均不以零开头,除非是数字 0 本身。不能使用任何标准库的大数类型(比如 BigInteger)或直接将输入转换为整数来处理。
示例:
输入:num1 = “99”, num2 = “99”
输出:”9801”
思路:
整型直接相乘会产生溢出错误。模拟两数手动相乘的过程。两数相乘时,乘数某位与被乘数某位相乘产生结果存入结果数组中:乘数 num1 位数为 n,被乘数 num2 位数为 m,num2 x num1 结果 result 最大总位数为 m+n,num1[i] x num2[j] 的结果为 tmp (位数为两位,”0x” 或 “xy” 的形式),其第一位位于 result[i+j],第二位位于 result[i+j+1]。

res[i + j] += sum / 10; 可能产生进位(result 数组元素大于 10)。i+j 是最终结果的高位,i+j+1 是低位。由于计算顺序是从右往左、从低到高的,所以每一轮都不需要考虑高位是否要进位,下一轮自然会去处理(下一轮此高位就变成了低位)。对于 索引为 0 处的值(最后一次相加),因为 result[0] = 0,所以无论最后相加的两个数多大都不会产生进位,最后一次相加不产生进位即可。
题解:
class Solution {
public String multiply(String num1, String num2) {
if (num1.charAt(0) == '0' || num2.charAt(0) == '0') return "0"; // 当某数为0则直接返回0,否则结果数组转换为字符串会多出0
int[] result = new int[num1.length() + num2.length()];
for (int i = num1.length() - 1; i >= 0; i--) {
int ele1 = num1.charAt(i) - '0';
for (int j = num2.length() - 1; j >= 0; j--) {
int ele2 = num2.charAt(j) - '0';
int mult = ele1 * ele2 + result[i + j + 1]; // 需要加上低位的数
result[i + j + 1] = mult % 10; // 低位:考虑进位
result[i + j] += mult / 10; // 高位:不考虑进位
}
}
StringBuilder resString = new StringBuilder();
if (result[0] != 0) resString.append(result[0]); // 舍去高位0
for (int i = 1; i < result.length; i ++) resString.append(result[i]);
return resString.toString();
}
}
tips:
- 时间复杂度:O(m * n),m, n 分别为 num1 和 num2 的长度
- 空间复杂度:O(m+n),用于存储计算结果
9. Palindrome Number 回文数
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
示例:
输入:x = 121ㅤ|ㅤx = -121
输出:trueㅤ|ㅤfalse
思路:
取出后半段数字进行反转。当 x 不大于 revert 时则表示后半部分反转数字已经对半或者过半(数字 x 的位数为奇数时),数字 x 的位数为偶数时也可能后半部分反转后的数字小于 x 则还会(最多)继续将后半部分数字位数多一位(此种情况只有等于 x 时才为回文数,故不影响最终结果)。
题解:
class Solution {
public boolean isPalindrome(int x) {
if (x < 0 || x % 10 == 0 && x != 0) return false; // 当x为负数或者个位为0但为两位以上数字时返回 false
int revert = 0; // 原数字 x 的后半部分反转后的结果
while (x > revert) {
revert = revert * 10 + x % 10; // 将x最后一位添加到revert末尾(取出最低位数字:对10取模)
x /= 10; // 舍去x最后一位:除以10后取整
}
return x == revert || x == revert / 10; // x 位数为奇数时,原数最中间的数字就在revert的最低位上,则revert需要除以10
}
}
tips:
- && 运算符的优先级高于 ||;
- 时间复杂度:O(logn)
- 空间复杂度:O(1)
7. Reverse Integer 整数反转
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。如果反转后整数超过 32 位的有符号整数的范围 [−2^31, 2^31 − 1] ,就返回 0。假设环境不允许存储 64 位整数(有符号或无符号)。-2^31 <= x <= 2^31 - 1。
示例:
输入:x = -123
输出:-321
思路:
定义变量 result 初始值为 0 ,代表反转后的 x 的值。对 x 不断进行取模除以10的操作以取出其每位的数字 digit ,对于 result 不断进行乘以 10 加上 x 当前位数上的数字 digit 的操作以得到 x 反转的中间结果。每次转换 result 的中间结果前需要判断当前转换是否越界:result * 10 + digit 是否会超过 int 类型的范围(当会越界则直接返回 0)。
对于负数也适用:负数对正数取模的运算规则为商 q 与除数 n 的乘积为第一个大于被除数的整数(在数论中商 q 与除数 n 的乘积为第一个小于被除数的整数),由商则可得出模值(余数),也即负数取模正数的结果为这个负数的绝对值取模这个正数后加上一个负号。digit 变为负数 x 的最后一位加上符号,result 累加时也总是将之前的中间结果(负数)乘以 10 再加上一个负数。
题解:
class Solution {
public int reverse(int x) {
int result = 0;
while (x != 0) { // 当 x = 0 代表 x 的所有位数均已取出
int digit = x % 10; // 当前x的个位数
if (result > Integer.MAX_VALUE / 10 || result == Integer.MAX_VALUE / 10 && digit > Integer.MAX_VALUE % 10) return 0; // 转化为逆序会发生越界,则直接返回0
if (result < Integer.MIN_VALUE / 10 || result == Integer.MIN_VALUE / 10 && digit < Integer.MIN_VALUE % 10) return 0;
result = result * 10 + digit;
x /= 10; // 对x通过不断取模并除以10的方式求出其每位上的数字
}
return result;
}
}
tips:
- 时间复杂度:O(logn),翻转的次数即 x 十进制的位数
- 空间复杂度:O(1)
8. String to Integer (atoi) 字符串转换整数 (atoi)
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数(类似 C/C++ 中的 atoi 函数)。函数 myAtoi(string s) 的算法如下:读入字符串并丢弃无用的前导空格;检查下一个字符(假设还未到字符末尾)为正还是负号,读取该字符(如果有)。 确定最终结果是负数还是正数。 如果两者都不存在,则假定结果为正;读入下一个字符,直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略;将前面步骤读入的这些数字转换为整数(即,”123” -> 123, “0032” -> 32)。如果没有读入数字,则整数为 0 。必要时更改符号(从步骤 2 开始);如果整数数超过 32 位有符号整数范围 [−2^31, 2^31 − 1] ,需要截断这个整数,使其保持在这个范围内。具体来说,小于 −2^31 的整数应该被固定为 −2^31 ,大于 2^31 − 1 的整数应该被固定为 2^31 − 1 ;返回整数作为最终结果。注意:本题中的空白字符只包括空格字符 ‘ ‘ ;除前导空格或数字后的其余字符串外,请勿忽略 任何其他字符。0 <= s.length <= 200。s 由英文字母(大写和小写)、数字(0-9)、’ ‘、’+’、’-‘ 和 ‘.’ 组成。
示例:
输入:s = “ -42”ㅤ|ㅤs = “words and 987”ㅤ|ㅤs = “-91283472332”
输出:-42ㅤ|ㅤ0ㅤ|ㅤ-2147483648
题解:
class Solution {
public int myAtoi(String s) {
String numStr = s.trim();
int result = 0;
int index = 0;
int signed = 1;
if (index < numStr.length() && (numStr.charAt(index) == '+' || numStr.charAt(index) == '-')) {
signed = numStr.charAt(index) == '-' ? -1 : 1;
index++;
}
if (index < numStr.length() && (numStr.charAt(index) < '0' || numStr.charAt(index) > '9')) return result;
while (index < numStr.length() && numStr.charAt(index) >= '0' && numStr.charAt(index) <= '9') {
int digit = numStr.charAt(index++) - '0';
if (result > Integer.MAX_VALUE / 10) return signed == 1 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
if (result == Integer.MAX_VALUE / 10) {
if (signed == 1 && digit > Integer.MAX_VALUE % 10) return Integer.MAX_VALUE;
if (signed == -1 && -digit < Integer.MIN_VALUE % 10) return Integer.MIN_VALUE;
}
result = result * 10 + digit;
}
return signed == 1 ? result : -result;
}
}
tips:
- 判断是否越界的思路与7题相似;
- 时间复杂度:O(n),n 为字符串的长度
- 空间复杂度:O(1)
191. Number of 1 Bits 位1的个数
请实现一个函数,输入一个整数(以二进制串形式),输出该数二进制表示中 1 的个数。例如,把 9 表示成二进制是 1001,有 2 位是 1。因此,如果输入 9,则该函数输出 2。
示例:
输入:11111111111111111111111111111101(有歧义,实际输入为 -3)
输出:31
思路:
位运算。
解法一:题目输入的为带符号int范围的整数(题目有歧义,并非题目描述里的二进制串;且考虑有符号数,即不能使用遍历模2在除2的方式求每位的数),求解其补码二进制串中1的个数(当输入为负数时符号位1也需要考虑到结果中)。初始化一个用于进行位与运算的常数con=1,遍历32次(int类型的位数),每次循环体内 n & con 位与运算,每一次遍历后将con位运算左移1位(当前遍历的位为1,其他位都为0),当 n&con 不等于0则代表原数 n 当前位为1(即使原数n为负数,遍历到符号位位与运算的结果为10000000000000000000000000000000,其表示-2^31也不为0),即可求出原数二进制表示中 1 的个数。
解法二:对于 n & (n - 1) ,其运算结果恰为把 n 的二进制中最低位的 1 变为 0 之后的结果。只要每次执行这个操作,就会消除掉 n 的二进制中最后一个出现的 1。因此执行 n & (n - 1) 使得 n 变成 0 的操作次数,就是 n 的二进制中 1 的个数。对于负数也适用。
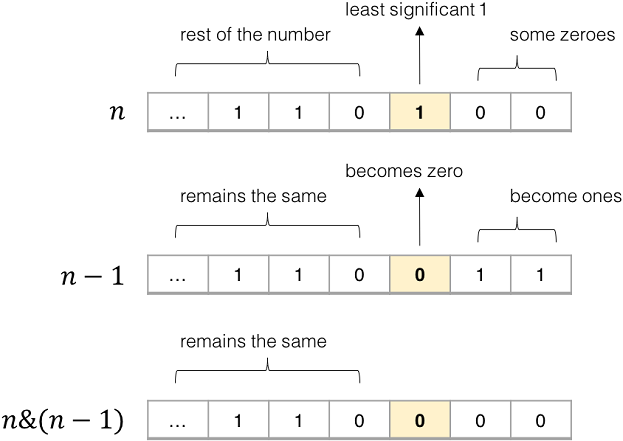
题解:
class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int result = 0;
while (n != 0) {
n &= n - 1;
result++;
}
return result;
}
}
/*class Solution {
// you need to treat n as an unsigned value
public int hammingWeight(int n) {
int result = 0;
int con = 1;
for (int i = 0; i < 32; i++) {
if ((n & con) != 0) result++; // != 的优先级高于 &
con <<= 1;
}
return result;
// return Integer.bitCount(n); // 库函数
}
}*/
tips:
- 调用库函数 java.lang.Integer类中的static int bitCount(int i) 方法,返回指定 int 值的二进制补码表示形式的 1 位的数量。当输入为负数时也满足题意;
- 时间复杂度:O(32),解法一;O(k),k为整数n二进制中1的个数,解法二
- 空间复杂度:O(1)
231. Power of Two 2 的幂
给你一个整数 n,请你判断该整数是否是 2 的幂次方。如果是,返回 true ;否则,返回 false 。如果存在一个整数 x 使得 n == 2^x ,则认为 n 是 2 的幂次方。不使用循环/递归解决此问题。
示例:
输入:n = 16
输出:true
思路:
思路与191题相似。当 n 小于等于 0 则一定不是 2 的幂,其次对于 2 的幂次方的数 n,其二进制补码表示形式的 1 位的数量一定为1个。对于 n & (n - 1) ,其运算结果恰为把 n 的二进制中最低位的 1 变为 0 之后的结果。故执行一次 n & (n - 1) 判断其结果是否等于 0,如果为 0 则代表 n 二进制补码表示形式的 1 位的数量为1个(即为 2 的幂次方)。
题解:
class Solution {
public boolean isPowerOfTwo(int n) {
return n > 0 && (n & n - 1) == 0;
}
}
tips:
- 时间复杂度:O(1)
- 空间复杂度:O(1)
60. Permutation Sequence 排列序列
给出集合 [1,2,3,...,n],其所有元素共有 n! 种排列。给定 n 和 k,返回第 k 个排列。1 <= n <= 9,1 <= k <= n! 。
示例:
输入:n = 3, k = 3
输出:”213”
解释:按大小顺序列出所有排列情况,并一一标记,当 n = 3 时, 所有排列如下:”123”、”132”、”213”、”231”、”312”、”321”
思路:
数学。由n和k按位推导排列。eg:对于n=4, k=15 找到k=15排列的过程。

题解:
class Solution {
public String getPermutation(int n, int k) {
StringBuilder result = new StringBuilder();
List<Integer> candidates = new ArrayList<>(); // 候选数字集合
int[] factorials = new int[n + 1]; // 阶乘数组:factorials[i] = i!
factorials[0] = 1; // 0的阶乘为1
int base = 1; // 用于计算阶乘的辅助变量
for (int i = 1; i <= n; i++) {
candidates.add(i); // 候选数字需要从小到大有序加入集合
base *= i;
factorials[i] = base;
}
k--; // 从0开始计数
for (int i = n - 1; i >= 0; i--) {
int index = k / factorials[i]; // 候选数字的索引
result.append(candidates.remove(index));
k -= index * factorials[i];
}
return result.toString();
}
}
tips:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
118. Pascal’s Triangle 杨辉三角
给定一个非负整数 numRows,生成杨辉三角的前 numRows 行。在杨辉三角中,每个数是它左上方和右上方的数的和。
示例:
输入:5
输出:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
思路:
杨辉三角,是二项式系数在三角形中的一种几何排列。杨辉三角形第 n 层(顶层称第 0 层第 1 行,第 n 层即第 n+1 行,n 为包含 0 在内的自然数)正好对应于二项式 (a+b)^n 展开的系数。除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和(第 n 行第 k 个数字等于第 n-1 行的第 k-1 个数字与第 k 个数字的和)。
题解:
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> result = new ArrayList<>();
for (int i = 0; i < numRows; i++) {
List<Integer> row = new ArrayList<>();
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i) {
row.add(1);
} else {
row.add(result.get(i - 1).get(j - 1) + result.get(i - 1).get(j));
}
}
result.add(row);
}
return result;
}
}
tips:
- 时间复杂度:O(n^2);
- 空间复杂度:O(1),不考虑结果的空间占用
202. Happy Number 快乐数
编写一个算法来判断一个数 n 是不是快乐数。快乐数定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和;然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1;如果 可以变为 1,那么这个数就是快乐数。如果 n 是快乐数就返回 true,不是则返回 false 。
示例:
输入:19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
题解:
class Solution {
public boolean isHappy(int n) {
List<Integer> historyRes = new ArrayList<>();
while (true) {
int onceRes = digitsSquaresSum(n);
if (onceRes == 1) {
return true;
} else if (historyRes.contains(onceRes)) { // 陷入循环一定不是快乐数
return false;
} else {
historyRes.add(n);
}
n = onceRes;
}
}
private int digitsSquaresSum(int n) {
int result = 0;
while (n >= 1) {
int digit = n % 10;
result += digit * digit;
n = n / 10;
}
return result;
}
}
tips:
- 时间复杂度:O(logn),查找给定数字的下一个值的成本为 O(logn),因为需要处理数字中的每位数,而数字中的位数由 logn 决定;
- 空间复杂度:O(1)
724. Find Pivot Index 寻找数组的中心下标
给你一个整数数组 nums,请编写一个能够返回数组 “中心下标” 的方法。数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。如果数组不存在中心下标,返回 -1 。如果数组有多个中心下标,应该返回最靠近左边的那一个。中心下标可能出现在数组的两端。
示例:
输入:nums = [2, 1, -1]
输出:0
解释:下标 0 左侧不存在元素,视作和为 0,右侧数之和为 1 + (-1) = 0 ,二者相等。
题解:
class Solution {
public int pivotIndex(int[] nums) {
int post = 0, pre = 0;
for (int i = 0; i < nums.length; i++) {
post += nums[i];
}
for (int i = 0; i < nums.length; i++) {
post -= nums[i];
if (pre == post) return i;
pre += nums[i];
}
return -1;
}
}
258. Add Digits 各位相加
给定一个非负整数 num,反复将各个位上的数字相加,直到结果为一位数。
示例:
输入:38
输出:2
解释:各位相加的过程为3 + 8 = 11, 1 + 1 = 2。 由于 2 是一位数,所以返回 2。
思路:
当num的值大于10时,各个位上的数字相加到一位数时的结果为num对9取模(模为0时返回9)。举例来说,对于一个三位数’abc’,其值大小为s1 = 100 * a + 10 * b + 1 * c = 99 * a + 9 * b + a + b + c,经过一次各位相加后,变为s2 = a + b + c = 10 * x + 1 * y = 9 * x + x + y,再经过一次各位相加后,变为s3 = x + y = ‘一位数’(结果)。减小的差值为s1 - s2 = 99 * a + 9 * b 或者 s2 - s3 = 9 * x,差值可以被9整除,每一个循环都如此,故可以将原始数据num对9取模值即为结果(与此同时,当模值为0时即代表最后各个位上的数字相加结果为9)。
题解:
class Solution {
public int addDigits(int num) {
if (num < 10) return num;
return num % 9 != 0 ? num % 9 : 9;
}
}
tips:
- 时间复杂度:O(1)
- 空间复杂度:O(1)
204. Count Primes 计数质数
统计所有小于非负整数 n 的质数的数量。
思路:
使用埃拉托斯特尼筛法(埃氏筛),也称素数筛,来找出一定范围内所有的素数。由要筛数值的范围n,找出sqrt(n)以内的素数p1, p2, …, pk(序列中最大数小于等于最后一个标出的素数的平方,那么剩下的序列中所有的数都是质数),将每个素数的各个倍数,标记成合数。一个素数的各个倍数,是一个差为此素数本身的等差数列。先用2去筛,即把2留下,把2的倍数剔除掉;再用下一个素数,也就是3筛,把3留下,把3的倍数剔除掉;接下去用下一个素数5筛,把5留下,把5的倍数剔除掉;不断重复下去……。
题解:
class Solution {
public int countPrimes(int n) {
if (n <= 2) return 0;
boolean[] isPrime = new boolean[n];
Arrays.fill(isPrime, true); // 先假设所有小于n的整数都为质数
isPrime[0] = isPrime[1] = false; // 质数定义 > 1
int count = n - 2;
for (int i = 2; i <= Math.sqrt(n - 1); i++) {
if (isPrime[i]) {
for (int j = i * i; j < n; j += i) { // 等差数列
if (isPrime[j]) { // 防止重复标记
isPrime[j] = false;
count--;
}
}
}
}
return count;
}
}
tips:
- 时间复杂度:O(nloglogn)
- 空间复杂度:O(n)
